matma Paula ;))): W kwadracie ABCD wierzchołek A ma współrzędne (1,−3), a jedna z przekątnych zawiera się w prostej o równaniu 2x−y=0 Oblicz pole kwadratu

Paula ;))): Pomoże ktoś?

===:

prosta: 1. obliczyć odległość punktu A od przekątnej 2. Obliczyć długość przekątnej i pole rombu o danych przekątnych.

Paula ;))): A jak obliczyć te przekątne?

Janek191: A = ( 1; − 3) 2 x − y = 0

	I 2*1 − 1*(−3) + 0 I		5
x =		=		= √5
	√22 + (−1)2		√5

d = 2 x = 2√5 Pole kwadratu P = 0,5 d² = 0,5*( 2√5)² = 0,5* 4*5 = 10 ===============================

Janek191: P = ( x₀; y₀) Równanie prostej : A x + B y + C = 0 Wzór na odległość punktu P od tej prostej :

	I A*x0 + B*y0 + C I
d =
	√A2 + B2

−−−−−−−−−−−−−−−−− W zadaniu było: A = 2 B = − 1 C = 0 x₀ = 1 y₀ = − 3

===: masz równanie prostej zawierającej jedną z przekątnych. y=2x Punkt A=(1, −3) nie należy do tej przekątnej. Wykorzystujesz fakt, że przekątne kwadratu przecinają się pod kątem prostym.

	1
Prosta prostopadła do prostej y=2x ma współczynnik kierunkowy a=−
	2

Piszesz równanie prostej o tym współczynniku i przechodzącej przez A

	1		1		1
y+3=−		(x−1) ⇒ y=−		x−2
	2		2		2

Teraz poszukaj punktu przecięcia się prostych zawierających przekątne dalej sama

Paula ;))): Ale ja mam tylko pole obliczyć i koniec

Paula ;))): tam pod tego x trzeba podstawić dowolną liczbę?

Paula ;))): Niech mi ktoś to napisze w jednej całości

prosta: 19.38 rozwiązane w całości

pa ;p: A skąd tam się wzieło 1?

prosta: 1. obliczasz odległość punktu A od prostej godz.19.31 2. Daje to nam połowę długości przekątnej kwadratu. Kwadrat jest rombem, stosujemy wzór na pole rombu z przekątnymi.

prosta: https://matematykaszkolna.pl/strona/1249.html

pa ;p: Czyli mam przepisać tylko rozwiązania Janka191?

prosta: musisz wiedzieć co tam jest napisane

pa ;p: To weź mi powiedz w jakiej kolejności mam to przepisać?

prosta:

	d
w rozwiązaniu Janka w trzeciej linijce trzeba by napisać "		=" zamiast "x="
	2

pa ;p: Weźcie napiszcie bo mnie denerwujecie wszyscy, bo wam to łatwo powiedziec

pa ;p: A czemu d/2

prosta:

	d
jeśli d to długość przekątnej kwadratu....do liczona odległość jest równa
	2

pa ;p: A czemu C wynosi 0?

Janek191: Poprawka do 19.38 w we wzorze na odległość punktu A od przekątnej kwadratu zamiast x napisz 0,5 d − połowa przekątnej kwadratu Wtedy 0,5 d = ... = √5 więc d = 2√5 Pole kwadratu P = 0,5 d² − jest taki wzór =========== O 19.41 napisałem Ci wzór na obliczanie odległości dowolnego punktu P =(x|₀, y₀) od dowolnej prostej o równaniu : A X + B y + C = 0

Janek191: 2 x − y = 0 lub 2 x − y + 0 = 0 A = 2 B = − 1 C = 0

pa ;p: ale chyba jak nie ma danego C to trzeba chyba je obliczyć a nie

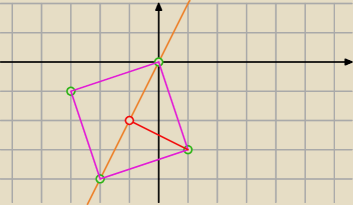
Janek191: Patrz na rysunek z 18.23 0,5 d − długość czerwonego odcinka Dana prosta narysowana jest kolorem pomarańczowym

pa ;p: Dobra zrobię to tak jak wy mi mówicie a jak bd źle to napiszę wam jak trzeba było zrobić

Janek191: Masz A x + B y + C = 0 2 x − 1* y + 0 = 0 więc A = 2 B = − 1 C = 0

prosta: Ax+By+C=0 2x+−1y+0=0 współczynniki odczytujemy z równania prostej.

Paula ;))): dziękuje wszystkim za zrobione zadanie. Mam pytanie tylko czy mam liczyć te przekątne? Czy tylko co napisałeś ty Janek?

prosta: nie musisz obliczać współrzędnych wierzchołków, a długości przekątnych masz policzone.