trygonometria Metis: sin2x+cos2x=0 sin2x+cos²x−sin²x=0 Z "1" sin2x+1−sin²x−sin²x=0 sin2x+1−2sin²x=0 /*(−1) sin²x−sin2x−1=0 Co mogę zrobić ?

Jack: sin 2x+ cos2x = 0 sin 2x = 2sinx cosx cos2x = cos²x − sin²x... stąd ...= 2sinx cosx + 2 cos²x − 1 = 0 2cos²x + 2sinxcosx −1 = 0 delta...

Eta: cos(2x)≠0 to tg(2x)= −1 ⇒ .........

Jack: @Eta no wlasnie tak mysle, czy dzielac przez cos2x nie usuwamy jakichs mozliwosci?

Eta: cos(2x) i sin(2x) nie mogą się jednocześnie zerować więc możemy dzielić obustronnie przez cos(2x)≠0 ( bez straty rozwiazań

Metis: sin2x=−cos2x / cos2x

sin2x
	=−1
cos2x

tg2x=−1 Nie lubię takiego dzielenia

Metis: Dzięki Eta

Eta: A ja "nie lubię" ..... np: ..........

Eta: Inny sposób cos(2x)= sin(−2x)

	π
sin(		−2x)=sin(−2x)
	2

.....................

Jack: @Metis potem juz z gorki... tg2x = −1

sin2x
	= −1
cos2x

stąd

2tgx
	= −1
1−tg2x

stąd tg²x − 2tgx − 1 = 0... delta

Metis: @Jack Wiem

Jack: Etamoglabys wyjasnic "nie moga sie jednoczesnie zerowac"...no nie moge tego nigdy ogarnac, wiem ze to tak dziala ; D

Eta: " z górki" ? ( po co ta "Δ" ?

	π
tak : tg(2x)=−1 ⇒ 2x= −		+kπ ⇒ x=............
	4

Jack: tia...faktycznie

Eta: Czy : 1+0 =0? i czy 0+1= 0? i wszystko jasne

Eta: "tia..."

Jack: moglabys zerknac na moje zadanie? https://matematykaszkolna.pl/forum/311529.html

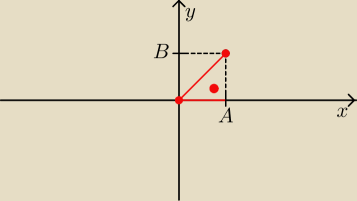
Dżin: Metis na takie zadania jest sprytny wzór: A*sin(x)+B*cos(x)=√A²+B²sin(x+α) gdzie α jest kątem zawartym pomiędzy dodatnią półosią OX a odcinkiem łączącym punkty (0,0) i (A,B) Czyli:

	π
sin(2x)+cos(2x)=√2sin(2x+		)
	4

a z takiej postaci łatwo odczytać rozwiązania

Kacper: Dżin na maturze musiałbyś go uzasadnić, potrafisz?

Dżin: Kacper Potrafię, oto dowód: z rysunku wiadomo, że:

	A		B
cosα=		oraz sinα=
	√A2+B2		√A2+B2

następnie: sin(x+α)=cosαsin(x)+sinαcos(x)

	A		B
sin(x+α)=		sin(x)+		cos(x)
	√A2+B2		√A2+B2

Podsumowując:

	A		B
√A2+B2sin(x+α)=√A2+B2*(		sin(x)+		cos(x))=A*sin(x)+B*cos(x)
	√A2+B2		√A2+B2