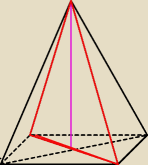
Stereo metria Jack: Przekroj ostroslupa prawidlowego czowrokatnego przechodzi wierzcholek −> przekatna podstawy Uzyskany trojkat jest rownoboczny o polu "P" Przedstaw objetosc...(za pomoca P oczywiscie) wg moich obliczen...skoro ten czerwony to P i jest rownoboczny...to skoro przekatna podstawy to a√2, no to krawedz boczna tego ostroslupa to tez a√2 wiec pole by musialo byc

	(a√2)2 * √3
P =
	4

	2P
i stad a2 =
	√3

ale wtedy nie wyjdzie dobry wynik

	2		√3 * P
powinno byc		P * √
	3		3

Jack: przynajmniej wg odp...

Jack: up...

Kacper: up up

Kacper: Pierwsza uwaga... liczysz pole podstawy jak pole trójkąta?

Jack: ? Pole trojkata...

Kacper: Dobra, zaraz policzę i dam rozwiązanie, o ile Eta mnie nie ubiegnie

utem: Dobrze liczy, to pole przekroju. Jack, licz dalej ,wszystko dobrze wychodzi.

	a√2
Możesz policzyć jako objętość dwóch ostrosłupów o podstawie P i wysokości
	2

a oblicz z tego wzoru, co wyznaczyłeś a².

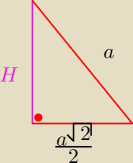
Jack: to wysokosc oblicze z (patrz rysunek) stad

	6 a2
H2 =
	4

Podstawiajac tamto a² H = √3 * P (gdzie P to pole tego trojkata rownobocznego − płaszczyzny)

Kacper: Przekrój jest trójkątem równobocznym, zatem

	a2√3
P=		, gdzie a to krawędź boczna ostrosłupa.
	4

	4P
Z tego wynika, że a=√
	√3

	d2		4P		2P
Liczymy pole podstawy: Pp=		=		=
	2		2√3		√3

	a√3		2√P*√3   4√3		√P*√3
Wysokość ostrosłupa: H=		=		=
	2		2		4√3

Objętość:

1

1

2P

√P*√3

2P

√P

V=

*Pp*H=

*

*

=

*

3

3

√3

4√3

3

4√3

Zaraz sprawdzę, czy wszystko ok

Jack: @Kacper...skad masz ze "a" to krawedz boczna ostroslupa...skoro przekroj to trojkat rownoboczny o boku a√2, bo przekatna kwadratu...

Kacper: Ja sobie przyjąłem a jako krawędź boczną ostrosłupa, bo z twoimi oznaczeniami, to tylko się miesza wszystko.

Jack: no ja tez... skoro a to krawedz boczna ostroslupa to przekatna kwadratu to a√2 czyli bok tego trojkata rownobocznego stad

	(a√2)2*√3
P =
	4

Kacper: Nie rozumiesz... Skoro a to krawędź boczna, to przekątna podstawy to też a. Ty piszesz, że to a√2.

Jack: a, faktycznie pardon...ja przyjalem "a" jako krawedz podstawy ostroslupa...wtedy krawedz boczna to a√2

Kacper:

Jack: aczkolwiek nadal mi owy wynik nie wychodzi...

	2P		P * √3		2P
mi wyszlo		* √		czyli wlasciwie		* √P
	3		√3		3

Kacper: Zrób jeszcze raz rysunek i podaj obliczenia, lub chodź na gg

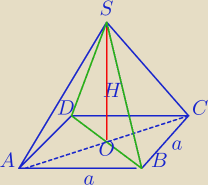
utem: Wg Twojej pierwszej koncepcji: P_ΔBDS=P

	1
V=		*a2*H
	3

|DB|=a√2

	(a√2)2*√3
P=
	4

	2P
a2=
	√3

a=√^2P_√3

	(a√2)√3		√6
H=		=		*√2P√3
	2		2

	1		2P		√6
V=		*		*		*√2P√3=
	3		√3		2

	P*√2		P*√2
=		*√2P√3=		*√2*√P√3=
	3		3

	2P
=		*√P*√33
	3

====================

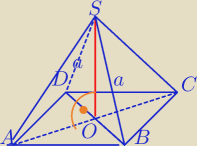
utem: II sposób. Rozcinamy ostrosłup wzdłuż podanego przekroju: Ozn. DB=a

	1		2P		a
V=2*		*PΔBDS*|OA|=		*P*
	3		3		2

a2*√3
	=P
4

	4P
a2=
	√3

a=2√^P_√3

a
	=√P√3
2

	2P
V=		*√P√3
	3

====================

Kacper: 2 sposób mnie się podoba

utem: Dziękuję.

Jack: Dzięki wielkie