trapez
rozsz:
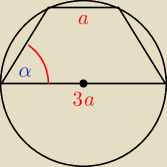
oblicz sinα
2 sty 19:20
rozsz: moge wykorzystac twierdzenie sinusow?
2 sty 19:26
Bogdan:
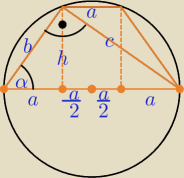
h
2 = b
2 − a
2 i h
2 = c
2 − 4a
2
| | c | |
c2 − b2 = 3a2 i c2 + b2 = 9a2 stąd c = ... i sinα = |
| |
| | 3a | |
2 sty 19:38
Eta:
Podaję inny sposób rozwiązania ( korzystam z rys.
Bogdana
h
2=a*2a ⇒ h= a
√2 to b=
√a2+h2=
√a2+2a2= a
√3
| | h | | a√2 | | √6 | |
sinα= |
| = |
| = |
| |
| | b | | a√3 | | 3 | |
2 sty 22:35
Jack: Eta
Rownanie h
2 = a * 2a jest z :
2 sty 22:48
Eta:
tak
2 sty 22:56
Jack: To jak mowilem chyba nigdy nie ogatlrne podobienstwa...
Moglabys narysowac ktore do ktoeego? : /
2 sty 22:58
2 sty 22:59
Eta:
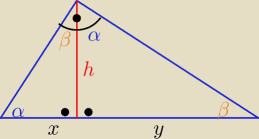
| h | | y | |
| = |
| ⇒ h2=x*y −− średnia geometryczna odcinków x i y |
| x | | h | |
2 sty 23:01
Jack: Omg...przeciez ja to na matmie udowadniałem...
2 sty 23:04
Eta:
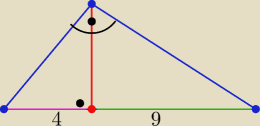
Oblicz pole i obwód tego trójkąta
2 sty 23:06
Eta:
To masz już
sklerozę ?
2 sty 23:06
Eta:
Czekam ..........na poprawne wyniki
2 sty 23:12
Jack: Nie, tylko ja to pitagorasem na okolo dowodzilem...
Czy jak pisze ze trojkaty sa podobne...to musze z jakiej cechy?
2 sty 23:12
Eta:
(kkk)
2 sty 23:13
Jack: h = 6
P = 13*3 = 39
2 sty 23:13
Jack: No tak ale chodzi mi na maturze napiaac skad wiem ze sa podobne?
2 sty 23:13
Eta:
trójkąt po lewej podobny do trójkąta po prawej z cechy (kkk)
| bok na przeciw α | | bok na przeciw α | |
| = |
| |
| bok na przeciw β | | bok na przeciw β | |
2 sty 23:16
Eta:
No chyba to wiesz,że α+β=90o ?
2 sty 23:17
Jack: No tak tak...jak najbardziej rozumiem tylko sie nie rozumiemy
Chodzi mi oto ze jak na maturze zobacze zadanie gdzie beda trojkaty podobne to musze napisac
"trojkaty taki i taki sa podobne z cechy takiej i takiej wiec..." czy wystarczy "trojkaty taki
i taki sa podobne wiec..."
2 sty 23:21
Eta:
Koniecznie trzeba pisać z jakiej cechy
2 sty 23:24
2 sty 23:25
Jack: Aaaa bo ja zazwyczaj nwm z jakiej korzystam ale pisze ze sa podobne...
2 sty 23:25
Eta:
Przeczytaj .... cechy ( w tablicach wzorów.... też są
2 sty 23:26