Znaleźć ekstrema o ile istnieją oraz określić przedziały monotoniczności funkcji Karolina: y=x*(3−x)²

qulka:

Jerzy: oblicz pochodną

Karolina: y'=x'*(3−x)² + x*(3−x)²' 1*9−x²+x(0−2x) 9−x² − 2x² = 0 ?

Kacper: Kombinujesz, nie umiesz policzyć dobrze pochodnej iloczynu, to po co w nią brniesz? Najpierw napisz ile to jest (3−x)² ?

Karolina: 3

Kacper: Jeszcze raz Oblicz (3−x)²

Karolina: nie wiem jak

Kacper: To poczytaj tutaj 55 i wróć

Karolina: dobrze, dziekuję

Karolina: x²+6x+9 ?

Dawid: Prawie dobrze x²−6x+9

Karolina: Proszę o podpowiedź co dalej?

Dawid: To więc jaki jest wynik x*(3−x)² = ?

Karolina: x³−6x²+9x

Dawid: określ dziedzinę i policz pochodną

Jack: @Dawid oj meczysz ja, meczysz xD f(x) = x(3−x)² = x(9 − 6x + x²) = x³ − 6x² + 9x f ' (x) = 3x² − 12x + 9 3x² − 12x + 9 = 0 delta...

Dawid: By było mniej męczenia Liczymy pochodną Przyrównujemy do zera Rysujemy wykres i odczytujemy z wykresu ekstrema

Dawid: oraz monotoniczność

Karolina: ale ja chcę żeby męczyć, wtedy zrozumiem a tak na szybko nie wiem o co chodzi

Dawid: To jak chcesz się pomęczyć ze mną to fajnie To podaj dziedzinę, a następnie pochodną

Karolina: D: x∊R y'=3x²−12x+9 ? dziękuję

Dawid: tak i teraz z tego policz pochodną i przyrównaj do zera i podaj wynik. Następnie narysuj wykres pochodnej będzie to funkcja kwadratowa. Niestety muszę wychodzić będę za 2 godziny ale pewnie ktoś się już dobierze do zadania i kto inny pomorze jak nie to pomogę

Dawid: pomoże

Karolina: y' = 0 ⇒ 3x²−12x+9 = O Δ=36 x₁=1 x₂=3

Jack: narysuj sobie parabole, zaznacz miejsca zerowe : D

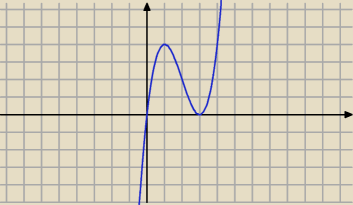
Karolina: ymax(1)=4 ymin(3)=0

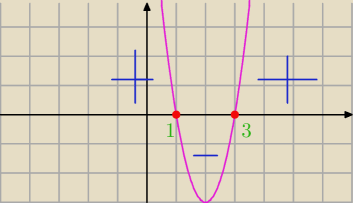
Jack: wykres nad osią + wykres pod osią −

KarolinaHa: rośnie ( −∞,1) (3,∞) maleje (1,3)

Jack: dobrze

KarolinaHa: IIIIIggggggiiiiiiiiiibbbbuuuuuuuuuuuuu! Dziękuję, jesteście Kochani Zrobimy jeszcze?

Jack: co do zapisu...nie mozesz pisac rosnie i potem dwa przedzialy albo cos, trzeba (−∞,1) funkcja rośnie (3,∞) rośnie (1,3) maleje

KarolinaHa: dobrze

Jack: bo jak bys napisala rośnie ( −∞,1) U (3,∞) to jest ewidentny blad, bo jak spojrzysz na wykres to na jedynce ma wartsosc (jak sama napisalas) 4, na trojce ma 0 , a z czworki do zera nic nie rosnie, najwyzej moze zmalec

KarolinaHa: oraz?

Jack: oraz?

Jack: tez juz sie zmywam, bd za ok. 2h

KarolinaHa: Odpowiedź: y_max(1)=4, y_min(3)=0; Funkcja rośnie w przedziałach (−∞;1) oraz (3;∞), maleje w przedziale (1;3) o "oraz" w odpowiedzi pytałam nieskładnie.

Jack: Oraz tez odpada...po prostu fubkcja rosnie... Funkcja rośnie... Funkcja maleje... Musisz kilka razy powiedziex xd

KarolinaHa: ok, dziękuję

KarolinaHa: To teraz bardzo proszę o rozwiązanie i objaśnienia krok po kroku: Znaleźć najmniejsze i największe wartości funkcji o ile istnieją. y=5+2x²−x⁴ x∊[−2,2]