stycznee
milo: Punkt symetryczny do punktu o współrzędnych (1, 1) względem prostej przechodzącej przez
punkty o współrzędnych (1, 2) i (3, −1)
(a) jest punktem przecięcia prostych o równaniach y =2x/3 i y=13/15
b)jest punktem przecięcia prostych o równaniach y=2x/3 +1/3 i y=21/13
c)ma współrzędne (25/13,21/13)
d)jest współliniowy z punktami o współrzędnych (7/2,0) i (0,7/3)
10 gru 21:50
5-latek:
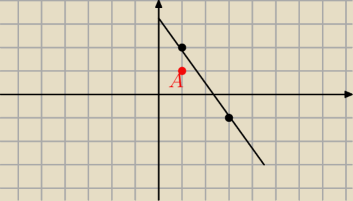
N o to policz jakie ma wspolrzedne ten punkt symetryczny
10 gru 21:57
Eta:
odp : b)
10 gru 21:59
Jolanta: c mi wyszło
10 gru 23:17
Eta:
@ Jolanty
Tak racja pomyłkowo wpisałam b)
poprawna odp : c)
10 gru 23:26
10 gru 23:27
Mila:
Tak, odpowiedź (c). Też się pomyliłam w rachunkach na samym końcu.
10 gru 23:34
Jolanta: moze krócej mozna ale napiszę Ci jak zrobiłam
| | 3 | | 7 | |
prosta przechodząca przez te punkty y=− |
| x+ |
| |
| | 2 | | 2 | |
| | 2 | | 2 | | 1 | |
przechodząca przez (1,1) ma wspólczynnik a= |
| y= |
| x+ |
| |
| | 3 | | 3 | | 3 | |
| | 19 | | 17 | |
punkt przeciecia prostych ( |
| ; |
| to środek odległosci miedzy punktami |
| | 13 | | 13 | |
(1,1) i (x
2,y
2)
| | x1+x2 | |
podstawiam do xS= |
| i yś....... |
| | 2 | |
10 gru 23:37
Mila:
Tak, Jolanto, ja też tak w końcu obliczyłam, ale rachunki są niewdzięczne, a to test
wyboru,
często można całości uniknąć, pokazałam sposób.
Może tu lepiej tradycyjnie, ale test wyboru nie powinien być tak układany, że obliczenia na
"full".
Musi Milo, to przećwiczyć.
10 gru 23:43