Punkt styczny z prostą !!! milo: Punkt symetryczny do punktu o współrzędnych (1, 1) względem prostej przechodzącej przez punkty o współrzędnych (1, 2) i (3, −1) (a) jest punktem przecięcia prostych o równaniach y =2x/3 i y=13/15 b)jest punktem przecięcia prostych o równaniach y=2x/3 +1/3 i y=21/13 c)ma współrzędne (25/13,21/13) d)jest współliniowy z punktami o współrzędnych (7/2,0) i (0,7/3)

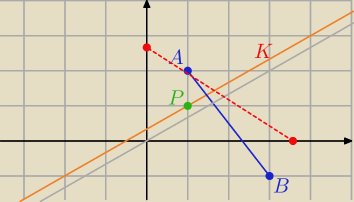
Mila: Punkt symetryczny do punktu o współrzędnych (1, 1) względem prostej przechodzącej przez punkty o współrzędnych (1, 2) i (3, −1). To jest test wyboru, zatem nie wymagane są wszystkie obliczenia,( byłoby sporo, postaraj się obliczyć , bo na maturze może być takie zadanie wśród otwartych ) Jednak coś musisz policzyć ,aby wybrać prawidłową odpowiedź. 1) Możesz odrzucić odp. (d), bo punkty leżą na osiach i pomocniczy rysunek . 2) możesz ustalić z rysunku wsp. kierunkowy prostej AB

	3
a=−		⇒prostopadła do AB ma wsp. kierunkowy:
	2

	2
a'=		jak podano w (a i b)
	3

2) narysować prostą

	2		1
k: y=		x+
	3		3

odp . (a) odpada, bo punkt P i P' leży na tej prostej.

	25
3)Liczymy wartość dla x=
	13

	2		25		1		50		13		69		23		21
y=		*		+		=		+		=		=		≠
	3		13		3		39		39		39		13		13

wykluczamy odp. (c) ======== zostaje (b)

Mila: No nie , mam błąd rachunkowy w (c) na samym końcu.. Czyli trzeba było sprawdzić (b) c)

	50		13		63		21
y=		+		=		=
	39		39		39		13

Wybieramy odpowiedź (c) Lepiej chyba tradycyjnie obliczać. Mam nadzieję, że umiesz znaleźć punkt symetryczny względem prostej.

Eta:

	3		7
k=AB : y= −		x+
	2		2

	2		2		1
p⊥k p: y=		(x−1)+1 ⇒ p: y=		x+
	3		3		3

	19		17
k ∩ p= S : ...... 4x+2=−9x+21 ⇒ x=		to 3y=2x+1 ⇒ y=
	13		13

	25		21
A'= (2xS−1 , 2yS−1)= S(		,		)
	13		13

zatem odp: c)

Mila: Myślałam Eto, że ustaliłaś odpowiedź , na drodze dedukcji., ale też liczyłaś jak 23:38.

Eta: Paskudne rachunki

Mila: Dobranoc

PW: Bez prostych. Symetria osiowa jest izometrią, więc zaczynamy od sprawdzenia: czy

	25		21
(1) odległość od (		,		) do (1, 2)
	13		13

jest taka sama jak (2) odległość od (1, 1) do 1, 2). Liczba (1) jest równa

	12		−5		144+25		13
√(		)2 + (		)2 = p{		)2 =		= 1.
	13		13		13		13

Liczba (2) też jest równa 1. Podobnie sprawdzamy odległości między

	25		21
(		,		) a (3, − 1)
	13		13

oraz między (1, 1) a (3, − 1 − obie są równe 2√2. Wniosek: odp. c) jest poprawna.

PW: te pierwiastki w 6. wierszu napisały mi się fatalnie, ale wiadomo o co idzie

Eta: A ja "lubię" proste

PW: Ja to gwoli przypomnienia "cyrklem i linijką", od tego zaczynamy w szkole podstawowej (punkt i jego obraz symetryczny jako wspólne punkty dwóch okręgów). Zawsze przypominasz, żeby nie armatą do muszki

Eta: