Analityczna. Ewka: 11) Punkty B(5;6) i D(−1;3) są końcami jednej z wysokości trójkąta równobocznego. a) Napisz równanie okręgu opisanego na tym trójkącie wiedząc, że D nie jest wierzchołkiem trójkąta b) Oblicz współrzędne pozostałych wierzchołków tego trójkąta c) Wyznacz współrzędne wierzchołków trójkąta A'B'C' , który jest obrazem trójkąta ABC w symetrii środkowej o środku w punkcie B. Proszę mi powiedzieć jak mam to zrobić każdy po kolei.

Ewka: Pomoże ktoś?

PW: a) W trójkącie równobocznym wysokości są też symetralnymi boków. Wiadomo, że środkiem okręgu opisanego na dowolnym trójkącie jest wspólny punkt symetralnych boków. W tym trójkącie środek okręgu jest więc wspólnym punktem wysokości. Znamy twierdzenie o tym, w jakim stosunku dzieli wysokości ich wspólny punkt. Korzystając z tego twierdzenia znajdziemy środek okręgu opisanego. Promień tego okręgu to odległość środka od wierzchołka trójkąta.

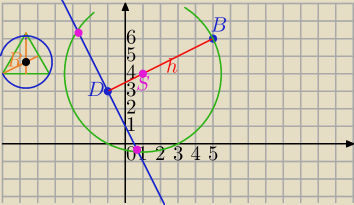
Mila: D jest spodkiem wysokości, jest środkiem boku AC. Wysokości przecinają się w jednym punkcie i w Δ równobocznym dzielą się w stosunku 1: 2 liczą od podstawy. S− punkt przecięcia wysokości, środek okręgu opisanego na tym Δ

	2
R=		h promień okręgu opisanego na Δ
	3

DB^→=[6,3]

1		1
	DB→=		*[6,3]=[2,1]=DS→
3		3

D(−1,3)→T{[2,1]⇒S=(−1+2,3+1)=(1,4) |DS|=√2²+1²=√5 R=2√5 a) Równanie okręgu ośrodku S(1,4) i r=2√5 (x−1)²+(y−4)²=(2√5)²⇔(x−1)²+(y−4)²=20 b) AC⊥DB, B(5;6) i D(−1;3) Równanie prostej DB y=ax+b 6=5a+b 3=−a+b −−−−−−−−−−odejmuję stronami 3=6a

	1
a=
	2

	1
y=		x+b
	2

Prosta AC: b: y=−2x+b, D∊b 3=−2*(−1)+b, b=1 b:y=−2x+1 Podstawić do równania okręgu i otrzymasz dwa punkty przecięcia prostej i okręgu, to będą wsp. szukanych wierzchołków. (x−1)²+(−2x+1−4)²=20⇔ (x−1)²+(−2x−3)²=20 (x−1)²+(2x+3)²=20 rozwiązuj c) B'=B Pozostałe A' i C' znajdujesz korzystając z tego, że B jest środkiem odcinków: AA' CC'

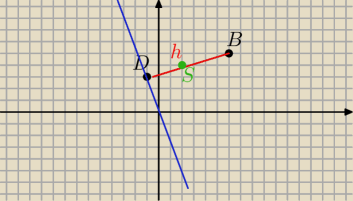
5-latek: Z geometrii elememtarnej wiemy ze : 1) wysokość w trojkacie równobocznym jest jednocześnie srodkowa , dwusieczna kąta i symetralna 2) Punkt przecięcia się wysokościw trojakacie dzieli wysokość w stosunku 2:1 licząc od wierzchołka 3. Pada pod kątem prostym na bok Wiec podpunkt a) Wyznaczyc dlugosc odcinka DB Wyznaczyc wspolrzedne punktu S który dzieli odcinek DB w stosunku 1:2 (sa tez wzory na to ) Wspolrzedne punktu S to srodek okrego opisanego na tym trójkącie Dlugosc odcinka SB to promien tego okręgu . Zrob najpierw to Punty D i B zaznaczyłem według danych reszta to rysunek poglądowy

5-latek: 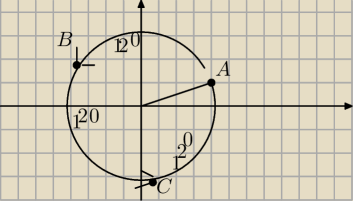Milu Jest to rysunek poglądowy . Chodzi o zasade jeśli mam trojkat równoboczny to każdy łuk ma miare 120^o Teraz mam dane wspolrzedne punktu A =(x,y) To wsporzedne punktu B=(x'y') mogę obliczyć ze wzoru x'=x*cos120^o−y*sin120^o y'= x*sin120^o+y*cos120^o natomiast wspolrzedne punktu C=(x'' y'') x''= x'*cos120^o−ysin120^o y''= x'sin120^o+cos120^o Albo podstawić wspolrzedne punktu A tylko ze wtedy będzie kąt 240 stopni

5-latek: Poprawie dla C x''= x'cos120^o−y'sin120^o y''= x'sin120^o+y'cos120^o

Mila: A kto to pamięta takie wzory? I w LO nie ma obrotów. Armaty do wróbli. Podałam prosty sposób.

5-latek: Wiem ze można tak jak Ty napisalas . Tez bym tak zrobil Ale zobacz (geometria na plaszcyznie Jakub zaznaczyl obrot rozszserzenie i studia

Mila: Rozwiązuje się zadania najprościej.

PW: Z obrotem też byłoby dobrze, ale trzeba całość przesunąć tak, by środek okręgu znalazł się w punkcie (0, 0) [podany wzór jest wzorem opisującym obrót wokół początku układu], a potem "wrócić" − chyba zbyt skomplikowane.

Eta: https://matematykaszkolna.pl/forum/306447.html

5-latek: Dobry wieczor PW Tak masz racje . Byloby dużo liczenia . Tak patrząc na rysunek Mili to nalezaloby przesunac punkt S i punkt B o wektor u=[−1,−4]

5-latek: Dziekuje CI bardzo Eta Wiem ze to było niedawno i szukałem tego