trygonometria samouk: Czy ktoś mógłby mi wyjaśnić jak dziecku z podstawówki skąd się bierze wzór że cos x = sin (π/2 − x) i inne temy podobne wzory? Znam zasady obliczania funkcji trygonometrycznych nietypowych kątów (np 315 czy 225), ale czy w moim przykładzie kąt x musi być kątem ostrym? Jak będzie zatem gdy będę mieć cos 4x = ? Prosze o pomoc w wyjaśnieniu? czy takie wzory są gdzieś "zebrane do kupy" ?

Janek191: Kliknij po lewej stronie ( kolor niebieski) na trygonometria

samouk: A który temat, bo w żadnym nie ma takiego wzoru...

PW: Wzory redukcyjne.

samouk: Mhm...ale ja prosiłam o wyjaśnienie SKĄD SIĘ BIERZE ten wzór? O jego wyprowadzenie...jakieś udowodnienie...poza tym we wskazanym temacie nie jest napiane czy mój x musi być kątem ostrym czy może być dowolnym...Poza tym we wskazanym temacie są wzory redukcyjne dotyczące każdego kąta i cos x nie zawsze będzie równy π/2 − x! Więc jeśli ktoś potrafi to jeszcze raz proszę o wyjaśnienie. W moim zadaniu nie wiem jakim kątem jest x (czy ma 20 czy 1200 stopni )

===: to w podstawówce jest już trygonometria

===:

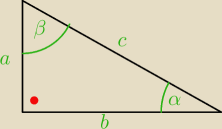
a		a
	=sinα ale jednocześnie		=cosβ a β=90−α
b		b

===:

	a		b
oczywiście miało być		i
	c		c

===:

a		a
	=sinα		=cosβ
c		c

samouk: Ok, ale jeszcze po raz trzeci zadam pytanie: czy kąt x MUSI być ostry? Pytałam też co jeśli x wynosi 1200 stopni? Albo jak wygląda wzór na cos 4x?

Eta: https://matematykaszkolna.pl/strona/430.html

PW: Z komentarzem: jeżeli we wzorze nie precyzuje się jaka musi być występująca w nim zmienna, to domyślnie przyjmuje się, że dowolna, Gdyby był wzór √x² = ­|x|, to pewnie nie pytałabyś, czy x musi być mniejsze od 7.

samouk: PW: Przedstawiony trójkąt nie jest dowolny tylko ostrokątny, dlatego pytam czy do każdego kąta (nawet 1200) mogę zastosować ten wzór? Eta, który zatem ze wskazanych wzorów byś użyła jeśli nie znam wartości kąta x i nie wiem z której jest ćwiartki

PW: Masz odesłanie do wzorów redukcyjnych i komentarz, że obowiązują dla dowolnych kątów α. Dowód z trójkątem dotyczył oczywiście kąta ostrego. Chcesz wymusić wyprowadzenie wzorów dla dowolnych kątów? To jest forum poświęcone rozwiązywaniu zadań na podstawie znajomości teorii, a nie dowodzeniu twierdzeń.

samouk: Nie nie chcę niczego wymuszać. Skoro tak to rozwiąż zadanie sin2x + cos 4x = 0. Tylko jeśli użyjesz wskazanego przeze mnie wzoru to wyjaśnij dlaczego uznajesz że kąt x jest ostry (tego z zadania nie wiemy). A jeśli użyjesz wzoru redukcyjnego (?) to uzasadnij swój wybór.

PW: Marudzisz. Nie rozumiesz wzorów − w ich założeniach nic się nie mówi jakie mają być kąty, dlaczego uparcie pytasz o kąty ostre?

Eta: https://matematykaszkolna.pl/forum/308822.html

5-latek: Suma katow w trojkacie wynosi 180 ^o (oczywiście wewnętrznych Ponieważ w trojkacie prostokątnym jeden z katow wynosi 90 ^o to suma pozostałych katow wynosi 90^o czyli każdy z tych dwóch katow jest kątem ostrym Stad jeśli w trojkacie prostokątnym dany jest jeden z kątow ostrych to można wyznaczyć drugi kat ostry z ewzoru 1. α+β=90^o Okreslenie =========== Dwa katy których suma rowna się 90^o nazywamy dopełniającymi Teraz popatrz na rysunek kolegi === z 22:27

	b		b
masz tam ze cosα=		także sinβ=
	c		c

czyli cosα= sinα ============= ale ze wzoru (1) mamy ze β=90^o−α wiec cosα=sin(90−α) Już widzisz skad ten wzor i dlaczego musi być kąt ostry ?

samouk: dlatego że we wzorze mam π/2 − x (czyli kąt mniejszy od 90 czyli ostry). Dlatego pytam bo jeśli mi w zadaniu nie mówią jaki to kąt to dlaczego mam stosować wzór π/2 −x a nie np π +x Tak, nie rozumiem, dlatego proszę o wyjaśnienie. Po to chyba jest forum. Gotowa odpowiedż to sobie znajdę w książce na końcu. Ale jak widzę, ja marudzę, ale wszystkowiedzący czytający nie potrafią mi udzielić odpowiedzi.

Eta:

PW: Daleki jestem od uważania się za wszystkowiedzącego. Im jestem starszy, tym bardziej rozumiem jak mało wiem. Ale: czy zapis

	π
		− x
	2

oznacza, że ten kąt jest ostry? Podstaw np. x = 3π albo x = −4π i już nie myśl o kątach ostrych (chyba że w zadaniu wprost mówią: podany kąt jest kątem ostrym.

Mila: I po co te nerwy, ludzie Ci tłumaczą, a Ty wybrzydzasz. cos(34^o)=sin(90^o−34⁰)=sin(56^o) katy ostre i nie ma problemu ze znakiem cos(110⁰)=cos(90^o+20^o)=−sin20⁰ znak (−) bo 110^o to kąt II ćwiartki , funkcja cosinus w II ćwiartce jest ujemna. albo tak: c cos(110^o)=cos(180⁰−70^o)=−cos(70^o) bo 110^o to kąt II ćwiartki, cos(315) =cos(360−45)=cos45 znak (+) bo kąt 315^o to kąt IV ćwiartki , a cosinus jest dodatni albo tak : cos(315)=cos(270+45)=sin (45) funkcja przechodzi w kofunkcję i znak początkowejj funkcji (cosinusa, od niego zaczynaliśmy) sin( 225)=sin(180+45)=−sin(45) i znak (−) bo kąt 225^o to kąt III ćwiartki, a sinus jest tam ujemny. ============================= Najlepiej wpisuj przykłady, to zrozumiesz. Analizuj. Masz pytania?

Eta: https://matematykaszkolna.pl/strona/2019.html

samouk: Eta PRZEPRASZAM Dzięki za wskazanie przykładu. Mila: tak mam pytania: ile wynosi cos(4x) ? PW. Dokładnie o to mi chodzi. W zadaniu nie mówią jaki to kąt ! dlatego pytam czy cos x to zawsze będzie (π/2 −x)?

Kacper: cos(4x) ? Zależy jaki jest x. Niesprecyzowane pytanie.

5-latek: Najpierw przeczytaj swój pierwszy post co napisales Czy w moim przykładzie kat x musi być ostry ? . Nie wiem nie napisales przykładu . Skad mam wiedzieć o co chodzi . CHciales wyprowadzenia wzoru cox= sin(90−x) to dostales Tak jest jak się piszse byle jak Teraz jeśli chodzi o cos 4xto cos4x= cos (2x+2x) wzor na cos 2x znasz i zastosuj wzor cos(x+y) gdzie y=x

Mila: cos(4x) możesz zapisać w innej postaci, zależy do czego to jest potrzebne. np. cos(4x)=cos²(2x)−sin²(2x) albo

	π
cos(4x)=sin(		−4x)
	2

Napisz zadanie.

5-latek: Tez sobie to zapiszse