Wyznacz równanie ogólne symetralnej odcinka AB jeśli Michał: Wyznacz równanie ogólne symetralnej odcinka AB jeśli A(−4,5) B(6,1)

sushi_gg6397228: wiesz co to jest symetralna ?

Michał: jak to obliczyć krok po kroku?

sushi_gg6397228: czekam na odp na pytanie

Michał: prosta prostopadła do prostej zawierającej odcinek AB i przechodząca przez jego środek

sushi_gg6397228: to podałeś co masz policzyć: 1. srodek odcinka AB (punkt S) 2. prostą AB 3 prostą prostopadła do prostej AB i przechodzaca przez punkt S

Michał: pomożesz w obliczeniu?

sushi_gg6397228: 1. podstawic do wzoru na srodek

Michał: (1,3) to współrzędne środka odcnika

Michał: S= −4+6/2=1 5+1/2=3

sushi_gg6397228: S(1;3) 2. wzór na prostą przez dwa punkty https://matematykaszkolna.pl/strona/1223.html lub y=ax+b i układ równań

	yB−yA
lub na potrzeby zadania musimy policzyć tylko "a"=
	xB−xA

Mila: A(−4,5), B(6,1) Własność symetralnej odcinka: Każdy punkt symetralnej odcinka jest jednakowo odległy od końców tego odcinka. Niech P(x,y) będzie dowolnym punktem symetralnej, wtedy: wtedy √(x+4)²+(y−5)²=√(x−6)²+(y−1)² /²⇔ (x+4)²+(y−5)²=(x−6)²+(y−1)² rozwijasz wg wzorów skróconego mnożenia, redukujesz, porządkujesz i otrzymasz równanie symetralnej:

	5		1
y=		x+
	2		2

Michał: wybiorę układ równań [ 5= − 4a+b [1= 6a+b [4= 10a/4 odjąłem od górnej części dolną −2,5a

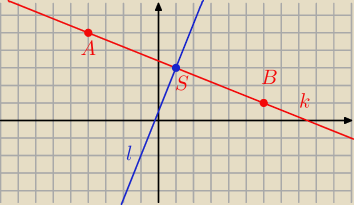
Janek191: A = ( − 4, 5) B = ( 6, 1)

	− 4 + 6		5 + 1
xs =		= 1 ys =		= 3
	2		2

S = ( 1; 3) pr AB y = a x + b 5 = − 4 a + b 1 = 6 a + b −−−−−−−−−− odejmujemy stronami 5 − 1 = ( − 4 a + b) − ( 6 a + b) 4 = − 10 a

	4		2
a = −		= −
	10		5

	2		8		17
b = 5 + 4 a = 5 + 4*( −		) = 5 −		=
	5		5		5

	2		17
k : y = −		x +
	5		5

====================== Prosta prostopadła

	5
y =		x + b oraz S = ( 1, 3)
	2

3 = 2,5*1 + b b = 0,5 y = 2,5 x + 0,5 ============ lub 2 y = 5 x + 1 l : 5 x − 2 y + 1 = 0 ================

Eta: No to jeszcze ja dorzucę

	1−5		2		5
S(1,3) aAB=		= −		to as=		bo AB ⊥ s i S∊s
	6+4		5		2

	5
s: y=		(x−1)+3 /*2 ⇒ s: 2y=5x−5+6
	2

s : 5x−2y+1=0 bingo

Eta: Jak widzę tu ciągle "układy równań" to mi się ( nóż w kieszeni otwiera

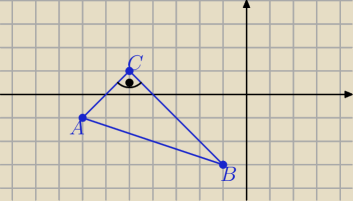
Michał: kolejne zadanie do obliczenia proszę o pomoc W trójkącie ABC wierzchołki mają współrzędne A(−7,−1) B(−1,−3) C(−5,1) a)wykaż że trójkąt ABC jest prostokątny b)Oblicz pole trójkąta ABC c)Oblicz pole koła opisanego na trójkącie ABC d)Napisz równanie prostej w której zawiera się środkowa CD

Michał: Eta czemu ci się nóż w kieszeni otwiera jak widzisz układy równań?

Eta: Prosty jest też sposób, który podała Mila chyba,że maturzysta nie umie wzorów uproszczonego mnożenia ?

Michał: no zgadza się,chciałbym przejść do zadania którego podałem o 17:59 liczę na pomoc

Eta: a) wystarczy wyznaczyć współczynniki kierunkowe :

	−3+1		1		1+1		1+3
aAB=		= −		i aAC=		= 1 i aBC=		= −1
	−1+7		3		−5+7		−5+1

a_BC* a_AC=−1 oznacza ,że proste zawierające przyprostokątne są prostopadłe

Eta:

Michał: w takim razie pkt a już jest teraz pozostałe pkt

Michał: jest ktoś kto pomoże?

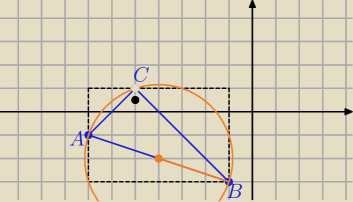
Eta: b) |AC|= 2√2 , |BC|= 4√2 i |AC|= √2²+6²=.........

	1
P=		*|AC|*|BC|= ......
	2

	1
c) P(k)= πR2 R=		|AC|=....
	2

P(k)=.....

Eta: d) sam włącz myślenie.............. powodzenia