Koło Ola: Środek sfery o promieniu 4 należy do sfery o promieniu 3. Oblicz długość okręgu będącego częścią wspólną obu tych sfer.

Eta: https://matematykaszkolna.pl/forum/177712.html

Eta: https://matematykaszkolna.pl/forum/35636.html

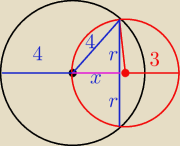
Janek191: x² + r² = 4² = 16 x + y = 3 ⇒ y = 3 − x y² + r² = 3² = 9 x² − y² = 16 − 9 = 7 x² − ( 3 − x)² = 7 x² − ( 9 − 6 x + x²) = 7 6 x − 9 = 7 6 x = 16

	8
x =
	3

więc

	64		144 − 64		80		16*5
r2 = 16 − x2 = 16 −		=		=		=
	9		9		9		9

	4
r =		√5
	3

Długość okręgu

	8
L = 2π r =		√5π
	3

==================

Ola: Dzieki wielkie

murarz tynkarz akrobata: Witam. Trochę odkopie zadanie. W treści mamy polecenie aby obliczyć długośc okręgu będącego częścią wspólną obu tych sfer. Według mnie to powinno znaczyć że liczymy tylko ten kawałek okręgu który znajduje się w środku sfery o promieniu r=4. Mógłby mi ktoś wytłumaczyc co rozumiemy pod pojęciem "długośc okręgu będąca częścią wspólną obu sfer?🙂

Adamm: dwie sfery przecinają się tworząc okrąg, mamy policzyć jego długość wydaje mi się że mylisz pojęcie sfery z pojęciem kuli

murarz tynkarz akrobata: Tzn liczymy okrąg tego koła które jest pośrodku. Tyle że to nie jest koło tylko jajo,

Adamm: nie, mamy policzyć długość okręgu, zapoznaj się dokładnie z pojęciami 1. koło 2. okrąg 3. sfera 4. kula to wszystko się od siebie różni

murarz tynkarz akrobata: Ok, już wiem thx