Dany jest trójkąt równoboczny ABC, w którym punkt D jest środkiem boku AB. Przez Royal: Dany jest trójkąt równoboczny ABC, w którym punkt D jest środkiem boku AB. Przez punkt D poprowadzono prostą pod kątem do boku AB, która przecięła bok BC w punkcie E takim, że pole trójkąta BDE jest równe ¹₈ pola trójkąta ABC. Wykaż, że α = 30°. Proszę o pomoc. Jest to zadanie 14 z matury rozszerzonej próbnej z Operonu. W kluczu odpowiedzi niestety jest sposób, którego nie rozumiem, a wiem, że jest około trzech sposobów żeby zrobić to zadanie.

Royal: #odświeżam

Royal: Pabc = ^a2√3₄ Pbde = ^a2√3₃₂ h= ^a√3₈ Co teraz?

Royal: Ktoś coś? Odpowiedź z klucza jest tutaj: http://arkusze.gieldamaturalna.pl/uploads/c3ab2ff2e1c0dbf4d06ae52ccf514a9eba90c18f.pdf Nie rozumiem trzeciej linijki

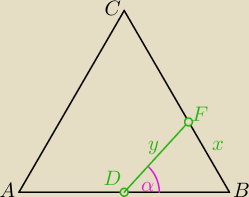
Tadeusz: to inny sposób ... nie wiem czy łatwiejszy

	a2√3		a2√3
SΔABC=		SΔDBF=
	4		32

	1		a		ax√3
ale jednocześnie SΔDBF=		*		*x*sin60o=
	2		2		8

stąd x=a/4 z twierdzenia cosinusów

	a2		a2		a		a		a√3
y2=		+		−2*		*		cos60o ⇒ y=
	4		16		2		4		4

z twierdzenia sinusów

x		y		a		a√3   4
	=		⇒		=
sinα		sin60o		4sinα		√3   2

	1
sinα=		⇒ α=30o
	2

Eta: https://matematykaszkolna.pl/forum/307135.html