monotonicznosc pochodne

monotonicznosc pochodne p: Zbadaj monotonicznosc funkcji y=e^x/x²−1 . Df to R z wykluczeniem 1 i −1 , czy tak ?

1 gru 12:41

J: tak

1 gru 12:42

p: a teraz pochodna tylko mam pytanie czy pochodna z e⁻x to e⁻x ?

1 gru 12:46

J: a gdzie tam masz: e^−x ?

1 gru 12:47

p: w liczniku jest emotka

ja tam moze zgubilam ten minus ale tam jest e⁻x/x²−1

1 gru 12:49

J: (e^−x)' = −e^−x

1 gru 12:50

p: e do potegi −x w liczniku

1 gru 12:50

p: aha dziekuje emotka

zaraz postaram sie obliczyc pochodna emotka

1 gru 12:50

p: czyli mi wyszlo ze pochodna jest rowna −x²e⁻x+e−2xe⁻x/(x²−1)²

1 gru 12:53

p: byc moze cos zle obliczylam , jesli tak prosze mnie poprawic

1 gru 12:54

	e^−x(x² + 2x − 1)
chaos ... f'(x) = −
	(x² − 1)²

1 gru 12:56

p: pochodna z 1 to 0 ? wiec na oncu w liczniku powinno byc 0 , nie tak ?

1 gru 13:00

p: aha juz znalazlam

1 gru 13:00

p: no tak i teraz musze przyrownac do zera ?

1 gru 13:00

J: nie ... ta jedynka bierze się z wyłączenia: e^−x przed nawias

1 gru 13:01

p: i teraz przyrownuje do zera ta pochodna ?

1 gru 13:02

J: nic nie musisz przyrównywać do 0 , bo nikt nie pyta ekstrema lokalne

1 gru 13:02

p: w liczniku jest rownanie kwadratowe czyli delta tak ?

1 gru 13:03

J: masz badać znak pochodnej , a on zależy od znaku wyrażenia: x² + 2x − 1, więc analizuj ( Δ jest przydatna )

1 gru 13:05

p: czyli x=−2√2 i x= √2/2 .

1 gru 13:08

p: z delty

1 gru 13:08

J: i co dalej ?

1 gru 13:09

p: nie wiem tego , musze wyznaczyc kiedy rosnie i kiedy funkcja maleje

1 gru 13:15

J: aby to stwierdzić musisz ustalić, kiedy pochodna jest dodatnia, a kiedy ujemna

1 gru 13:17

p: pochodna jest dodatnia kiedy jest x= √2/2 .a ujemna x=−2√2

1 gru 13:21

J: nie ..wtedy równa = 0

1 gru 13:22

p: aha czyli teraz tez nie rozumiem , jakie sa przedzialy monotonicznosci

1 gru 13:23

J: naszkicuj wykres pochodnej

1 gru 13:26

J: nie pochodnej .. tylko : x² + 2x − 1

1 gru 13:29

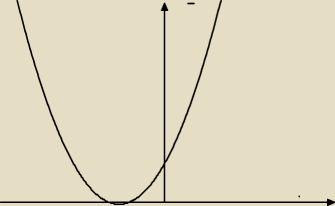
1 gru 13:38

p: taki wykres ?

1 gru 13:38

J: rozumiem,że przecina oś OX w dwóch punktach....kiedy wyrażenie jest dodatnie, a kiedy ujemne ?

1 gru 13:40

p: tego nie wiem emotka

1 gru 13:41

J: dla jakich x wykres leży nad osią OX ( jest dodatnie) , dla jakich pod ( jest ujemne ) ?

1 gru 13:42

p: nie lezy pod osią , tylko nad osią

1 gru 13:43

J: bzdura ... przecież ma dwa miejsca zerowe

1 gru 13:46

p: no tak , ma dwa miejsca zerowe pod osia te z minus 2√2 a nad osia ox to jest x=√2/2 , tak ?

1 gru 13:48

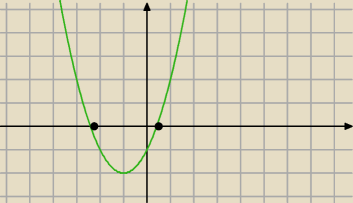
czarne kropki to miejsca zerowe.. kiedy : x² + 2x − 1 jest dodatnie, a kiedy ujemne ?

1 gru 13:58

p: dodatnie jest od − nieskonczonosci do czarnej kropki i od drugiej czarnej do + nieksonczonosci

1 gru 14:05

p: a ujemne jest od czarnej kropki pierwszej do drugiej czarnej kropki

1 gru 14:05

p: czyli dodatnie od 0 nieskonczonosc do − pierwiastek z 2 i od pierwiastek z 2/2 a ujemne od −2√2 do √2/2

1 gru 14:11

p: czy tak ?

1 gru 14:11

p: jesli nie to bardzo prosze o podanie poprawnej odpowiedzi

1 gru 14:12

J: oblicz " ile wynoszą kropki "

1 gru 14:13

p: te kropki to są te wartosci ktore obliczylam z delty tak ? x1 , x2 x1= √2/2 . x2=−2√2

1 gru 14:14

J: źle obliczyłaś

1 gru 14:20

p: gdzie jest błąd ? nie moge go znalezc

1 gru 14:26

J: ile wynosi Δ ?

1 gru 14:35

p: deltA WYNOSI pierwiastek z 8

1 gru 14:36

p: chyba ze zle obliczylam

1 gru 14:37

J: Δ = 2√2 .. .teraz: x₁ = ? , x₂ = ?

1 gru 14:38

p: x1 = −2√2 a x2= √2/2 , żle to jest ? wydaje mi sie ze dobrze oblizylam

1 gru 14:49

J: poczytaj to: https://matematykaszkolna.pl/strona/54.html

1 gru 14:50

p: tak obliczylam wg tych wzorów ,

1 gru 14:51

p: i jest błąd ? mnie sie wydaje ze ok sa obliczone miejsca zerowe emotka

1 gru 14:52

J: to pokaż te swoje obliczenia

1 gru 14:52

p: x1= −2−2√2/2*1 = −4√2/2 = − 2√2 x2==2+2√2/2*1= √2/2 tak obliczyłam

1 gru 14:54

J: Ty studiejesz i dla Ciebie : − 2 − 2√2 = −4√2 ? ... jestem w szoku

1 gru 15:00

p: to nie wiem jak powinno być ...

1 gru 15:01

	−2 + 2√2
x₁ =		= − 1 + √2
	2

x₂ = ... licz

1 gru 15:17

p: x2= −4 + √2/2 , tak ?

1 gru 15:22

J: a skąd masz − 4 ?

1 gru 15:24

mamniewidzialnylogin: tak emotka

1 gru 15:25

p: −2 − 2

1 gru 15:26

	−b −√Δ		−2 − 2√2
napij się wody ... x₂ =		=		= −1 − √2
	2a		2

1 gru 15:28

p: i to są te miejsca zerowe ?

1 gru 15:30

J: tak, to są te czarne kropki.. teraz zauważ,że pochodna jest dodatnia , gdy trójmian jest ujemny i odwrotnie ... i mozesz okreslać monotonoczność funkcji

1 gru 15:35