dowód geometria
dowodhelp: Dany jest kwadrat o boku a=6, w ten kwadrat wpisano trójkąt równoboczny w ten sposób, że
wierzchołek trójkąta jest wierzchołkiem kwadratu, a przeciwległy bok trójkąta jest równoległy
do przekątnej kwadratu. Wykaż, że bok trójkąta jest równy 6(√6 − √2 )
To jest zadanie 30 z matury próbnej operonu, w odpowiedzi jest równanie z proporcją, jednak nie
rozumiem skąd ono się wzięło... Mógłby ktoś pomóc?
30 lis 15:55
dowodhelp: :(
30 lis 17:49
30 lis 17:52
Eta:
Najłatwiejsze ... to dwa ostatnie moje wpisy
30 lis 17:53
dowodhelp: Dziękuję. Brakuje mi tutaj jakiejś wyszukiwarki zadań ; ).
30 lis 17:54
Eta:
U góry masz okienko .. szukaj (to wyszukiwarka forumowa)
wpisz .... "dany jest kwadrat" i .... zobaczysz to czego szukasz
30 lis 17:58
Janek191:
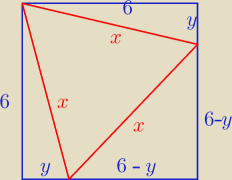
x
2 = 6
2 + y
2
x
2 = ( 6 − y)
2 + ( 6 − y)
2
−−−−−−−−−−−
2*( 36 − 12 y + y
2) − ( 36 + y
2) = 0
72 − 24 y + 2 y
2 − 36 − y
2 = 0
y
2 − 24 y + 36 = 0
Δ = 576 − 4*1*36 = 432 =144*3
√Δ = 12
√3
| | 24 − 12√3 | |
y = |
| = 12 − 6√3 |
| | 2 | |
x
2 = 36 + y
2 = 36 + 144 − 144
√3 + 108 = 288 − 144
√3 = 144*( 2 −
√3)
x = 12*
√ 2 − √3 = 6*
√ 8 − 4√3 = 6*(
√6 −
√2)
30 lis 18:02
30 lis 18:04
