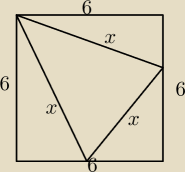
Trójkąt wpisany w kwadrat SonicDesu: Polecenie brzmi "Podaj x" Proszę o pomoc!

Janek191: x² = 6² + y² x² = 6² + y² x² = ( 6 − y)² + ( 6 − y)² −−−−−−−−−−−−−−−− x² = 36 + y² x² = 36 − 12 y + y² + 36 − 12 y + y² −−−−−−−−−− 36 + y² = 72 − 24 y + 2 y² y² − 24 y + 36 = 0 Δ = 576 − 144 = 432 = 3*144 √Δ = 12 √3

	24 − 12 √3
y =		= 12 − 6√3
	2

więc x² = 36 + (12 − 6√3)² = 36 + 144 − 144√3 + 108 = 288 − 144√3 = 144*( 2 − √3) zatem x = 12 √ 2 − √3 ≈ 6,24 ==============

Eta: x=6√2(√3−1)

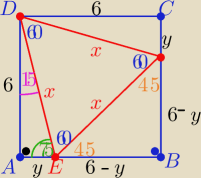
Eta: W trójkącie prostokątnym ADE

	6		6
cos15o =		⇒ x=
	x		cos15o

ze wzoru ( w tablicach) cos(α−β)=cosα*cosβ+sinα*sinβ cos15^o= cos(45^o−30^o) = cos45^o*cos30^o+sin45^o*sin30^o =

	√2		√3		√2		1		√2
=		*		+		*		=		( √3+1)
	2		2		2		2		4

	4
x= 6*		= ........... = 6√2(√3−1) [j]
	√2(√3+1)

Janek191: Tyle samo

Eta: Jasne,że "tyle samo" ale nie tak samo

PW: Wiedziałaś ile jest równy cos15°?

PW: O, o, dobrze się domyśliłem

Eta: @PW nie rozumiem pytania z 22:37

ICSP: Może inaczej: Sklejmy trójkąty AED oraz CDF bokami CD oraz AD. Dostajemy w ten sposób trójkąt równoramienny o kącie między ramonami 30^o oraz ramieniu długości x. Możemy z łatwością

	1
wyliczyć jego pole: P =		x2. POle trójkata BEF również można łatwo wyrazić za
	4

	1
pomocą: P2 =		x2. Dostajemy zatem równanie:
	4

1		1		x2√3
	x2 +		x2 +		= 36
4		4		4

	2 + √3
x2 *		= 36
	4

x² = 36 * 4 * (2 − √3} = 36 * 2 * (4 − 2√3) = 2 * 36² * (√3 − 1)² x = √2 * 6 * (√3 − 1)

PW: Pisząc moje pytanie widziałem tylko odpowiedź z 22:02 i domyślałem się, że zauważyłaś iż

	6
		= cos15°.
	x

Myślałem, że wzięłaś gotową wartość z tablic, bez liczenia − wtedy rozwiązanie jest "w jednej linijce".

Eta: W tablicach maturalnych nie ma "gotowego" cos15^o

SonicDesu: Dzięki wielkie za włożoną pracę, doceniam! Uratowaliście mi tyłek, nie miałem pomysłu na to zadanie Jeszcze raz dzięki!

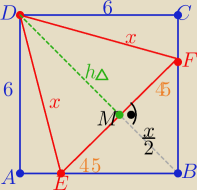
Eta: Jeszcze taki sposób ( na podstawę)

	x√3		x
|DM|=		, |BM|=		i |DB|=6√2
	2		2

|DM|+|BM| =|DB| ⇒ x√3+x= 12√2 ⇒ x(√3+1)=12√2 /*(√3−1) to 2x=12√2*(√3−1) ⇒ x=6√2(√3−1) [j]

Eta: Jeszcze inny sposób Na rys. wyżej : czworokąt EBFD jest deltoidem o przekątnych |BD|=6√2 i |EF|=x P(EFD)+P(EBF)=P(deltoidu)

x2√3		x2		6√2*x		4
	+		=		/*		, x>0
4		4		2		x

x(√3+1)=12√2 / *(√3−1}) ⇒ 2x= 12√2(√3−1) ⇒ x=6√2(√3−1) [j]