Funkcje cyklometryczne. :(: Pokaże ktoś metodę rozwiązywania równań cyklometrycznych na tym przykładzie? arctgx+arcctgx=π/2

sushi_gg6397228: to już było dzisiaj, poszukaj na forum

:(: Jakoś nie mogę tego znaleźć.

sushi_gg6397228: wpisałem arctg i wyszło https://matematykaszkolna.pl/forum/303554.html

:(: A mógłby ktoś rozwiązać ten przykład i podać odpowiedz, tam są tylko wskazówki. Nie robiliśmy w ogóle równań tego typu, pochodnych też jeszcze nie maiłem.

Godzio: Jakoś tak: arctgx = α ⇒ x = tgα arcctgx = β ⇒ x = ctgβ

	π		π
tgα = tgβ oraz α + β =		⇒ α =		− β
	2		2

	π
tg(		− β) = tg(β)
	2

π
	− β = β + kπ
2

	π
2β =		+ kπ
	2

	π		π
β =		+		* k
	4		2

x = 1

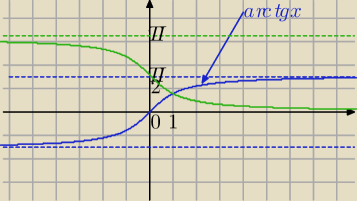
Mila: 1) Tożsamość:

	π
(1) arctgx+arcctgx=
	2

	π		π
arctgx=α gdzie: −		<α<		oraz arcctg(x)=β, gdzie :0<β<π⇔
	2		2

	π		3π
(2) −		<α+β<
	2		2

stąd:

	π
x=tgα i x=ctgβ⇔tgα=ctgβ⇔tgα=tg(		−β)⇔
	2

	π
α=		−β+kπ, k∊C⇔
	2

	π
α+β=		+kπ ⇔aby był spełniony warunek (2) to k=0⇔
	2

	π
α+β=		⇔
	2

	π
arctgx+arcctgx=		dla x∊R
	2

:(: Bardzo dziękuję za pomoc. Muszę chyba zmienić nick bo teraz to już nie wypada '':(''

Mila: Koniecznie zmień, bo łatwiej potem szukać swoich wpisów, gdy zachodzi potrzeba. A jeśli czegoś nie rozumiesz , to wpisuj problem, fragment, który chcesz lepiej zrozumieć.