pytanie ciekawa: jeśli mam taką nierówność 2|x+6|−|x|+|x−6|<18 rozwiązujemy ją w czterech przedziałach i czy jest różnica że np w pierwszym napiszę x∊<−∞;−6) a x∊<−∞;6>?

olekturbo: Jest.

olekturbo: Wyobraź sobie, że x = 5. Do pierwszego przedziału nie należy, natomiast do drugiego już tak

ciekawa: no ale potem nie zawrę 6 w przedziale, więc to chyba nie powinno mi robić różnicy

olekturbo: ?

ciekawa: i jeszcze mam pytanie czy opuszczanie modułu a zmiana znaków w każdym kolejnym przedziale jest związana z nawiasami?

ciekawa: chodzi że w 1 przypadku napiszę (−∞;−6) a w drugim <−6;0)

olekturbo: 1653

PW: <a, b> oznacza przedział domknięty, czyli taki do którego należą również krańcowe liczby a i b. −∞ czy +∞ nie są liczbami, przyjęło się pisać nawiasy otwarte (jak dla przedziału, do którego napisane końce nie należą, czyli (−∞, 6) oraz (−∞, 6> są napisami poprawnymi (i można liczbę 6 do tego przedziału zaliczyć albo do następnego − nie ma to znaczenia dla rozwiązania zadania), natomiast napisy z nawiasem "<" lub ">" przy nieskończonościach uznawane są za niepoprawne.

ciekawa: a potem gdy mam np x∊<−6;0) to czy fakt że jest to przedział lewostronnie domknięty wpłynie na to jak powinnam usunąć moduły do rozwiązania?

PW: Nie wpłynie, |x + 6| zmienia znak przy przejściu przez −6 (jest równe 0 dla x = −6). Obojętne do którego przedziału włączysz tę −6, byle raz − żeby się nie powtarzać. Niezależnie czy zastosujesz definicję modułu dla liczby ujemnej, czy dla nieujemnej, i tak wartość dla x = −6 jest równa zero: zarówno −(x + 6) = 0 jak i x + 6 = 0.

ciekawa: ok. A potem jak już liczę to w 1 przypadku piszę −2x−12+x−x+6<18 i chciałabym też wiedzieć co wpływa na taki zapis, bo jeśli nic to mogę zapisać to w 1 przypadku tak 2x+12+x−x+6<18, a w następnym tak z tą −2x−12. NIe mam pojęcia czy jest na to jakaś reguła czy piszemy tak by opuścić moduł na każdy sposob

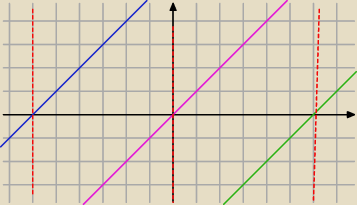
Aga1.: Oczywiście jest reguła. W przedziale (−∞,−6) wszystkie trzy funkcje przyjmują wartości ujemne, więc Ix+6I=−(x+6) IxI=−x Ix−6I=−(x−6) W drugim y=x+6 przyjmuje dodatnie, a pozostałe dwie ujemne Ix+6I=x+6 W trzecim wszystkie funkcje przyjmują wartości dodatnie, czyli Ix+6I=x+6 IxI=x Ix−6I=x−6

ciekawa: o dziękuję wykres jest bardzo pomocny