proszę o sprawdzenie
anna: Wyznacz zbiór wartości funkcji f :
| | 1 | |
a) f(x)= |
| , x ∊ <4 , 6> |
| | x2 +2x −24 | |
obliczyłam też
x
w = 2
f(2) = −1
| | 1 | | 1 | | 1 | |
dlaczego wynik w podręczniku jest że ZW f = < |
| . |
| > a nie < −1 , |
| > |
| | 15 | | 3 | | 3 | |
| | 1 | | π | | 5π | |
b) f(x) = |
| , x ∊ < |
| , |
| > ale ten przykład nie wiem |
| | sinx | | 4 | | 6 | |
wynik to ZW = <1 , 2>
15 paź 20:39
ICSP: xw ∉ [4,6] ?
15 paź 20:40
anna: ale dlaczego przecież x = 2
15 paź 21:08
sushi_gg6397228:
policz xw jeszcze raz
15 paź 21:12
anna: słusznie xw = −1 przepraszam za nieuwagę
a jak rozwiązujemy drugi przykład
15 paź 21:20
sushi_gg6397228:
widzisz, że xw ∉<4;6>, więc odp jest tak jak podali
15 paź 21:22
sushi_gg6397228:
robisz wykres sinusa i ograniczasz go do podanego przedziału−−> wykonać rysunek
15 paź 21:23
15 paź 21:24
anna: −1< 1sinx<1
0< 1sinx +1 i 1sinx −1 <0
1+sinxsinx>0 i 1 − sinxsinx <0
(1+sinx)(sinx)>0 i (1 − sinx)(sinx) <0
sinx>−1 i sinx>0 i 1< sinx i sinx <0
i nie wiem jak dalej aby otrzymać ZW <1.2>
15 paź 21:58
sushi_gg6397228:
dlaczego robisz po swojemu ?
15 paź 22:09
anna: wykres sobie narysowałam sinx i nie wiem jak ograniczyć do podanego przedziału−
15 paź 22:16
sushi_gg6397228:
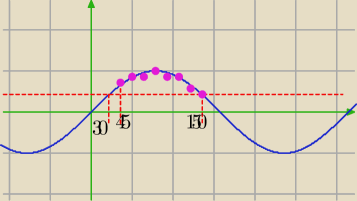
15 paź 22:18
sushi_gg6397228:
trzeba wymazać gumką niepotrzebny kawałek i zostawić ten z "różowymi kropkami"
15 paź 22:19
sushi_gg6397228:
wylicz "a; b" i podstaw poniżej
a ≤ sin x ≤ b
15 paź 22:23
anna: sin450 = √22 a sin1500 =12
czy te wartości mam podstawić za a i b
15 paź 22:35
sushi_gg6397228:
gdzie jest największa wartośc −−> nie widzisz to patrz na rysunek
15 paź 22:42
anna: największa wartość jest w 1
15 paź 22:51
sushi_gg6397228:
masz a= 0,5
b=1 i odp jak w 1−ym poście
15 paź 22:58
anna: dziękuję bardzo
15 paź 23:13
anna: podobne zad ktore mi nie wychodzi bo wynik jest ZW = <−2 , 2√33 >
f(x) = 1cosx , x∊< 3π4;4π3 >
cos 3π4 = − √22 a cos 4π3 = − 12
a ≤ sin x ≤ b
1a ≤ sin x ≤ 1b
zrobiłam też wykres ale nie wiem jak dojść do wyniku ZW = <−2 , 2√33 >
15 paź 23:33
anna: pomyliłam tam ma być
a ≤ cos x ≤ b
1a ≤ cos x ≤ 1b
15 paź 23:37
anna: jeszcze żle bo
1a ≤ 1cos x ≤ 1b
15 paź 23:39
ZKS:
−1 ≤ cos(x) ≤ 1
| | 1 | | 1 | |
−1 ≥ |
| ∨ |
| ≥ 1 |
| | cos(x) | | cos(x) | |
−2 < −
√2 < −1
| | 1 | | 3 | | 4 | |
Sprawdzamy czy |
| = −1 dla x ∊ [ |
| π ; |
| π] |
| | cos(x) | | 4 | | 3 | |
| | 3 | | 4 | |
x = π + k • 2π ∧ |
| π ≤ x ≤ |
| π ⇒ x = π. |
| | 4 | | 3 | |
Nasz zbiór nierówności to ZW
f = [−2 ; −1].
16 paź 00:03
ZKS:
Oczywiście zbiór wartości winno być.
16 paź 00:07
anna: `dziękuję bardzo
17 paź 17:35
anna: Wyznacz zbiór wartości funkcji f :
a) f(x)= 1x2−4x+3 x ∊ < 4 , 6>
f(4) = 13
f(6) = 115
xw = 2 ∊<4,6>
f(2) = −1
ZW = <−1, 13>
ale wynik to ZW =< 115, 13>
17 paź 17:45
sushi_gg6397228:
od kiedy 2 ∊ <4;6 >

17 paź 17:47
ZKS:
Takie pytanie do Ciebie, czy 2 należy do tego przedziału?
17 paź 17:49
anna: słusznie bo nie należy, bardzo przepraszam
za nieuwagę nie wiem czym się zasugerowałam
dziękuję za informację
17 paź 17:52

