wielomiany ania: |x²−2x|≥x³

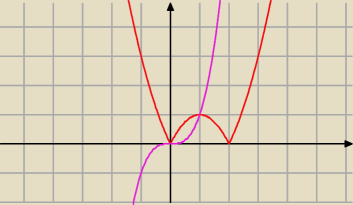
Aga1.: Graficznie x∊(−∞,1>

J: Algebraicznie: ⇔ x² − 2x ≥ x³ lub x² − 2x ≤ −x³

irena_1: |x²−2x|≥x³ x²−2x=x(x−2) 1) x∊(0; 2) −x²+2x≥x³ x³+x²−2x≤0 x(x²+x−2)≤0 x(x−1)(x+2)≤0 x∊(−∞; −2> ∪ <0; 1> x∊ (0; 1> 2) x∊(−∞; 0> ∪ <2; ∞) x²−2x≥x³ x³−x²+2x≤0 x(x²−x+2)≤0 Δ=1−8<0 x≤0 x∊(−∞; 0> Odp: x∊(−∞; 1>

Aga1.: @ J, czy tak można?

PW : Dla x < 0 prawa strona nierówności jest ujemna, a lewa nieujemna. Wszystkie liczby ujemne są więc rozwiązaniami. Liczba x = 0 jest rozwiązaniem, co sprawdzamy bezpośrednio. Wobec tego szukajmy dalszych rozwiązań dla x > 0. Nierówność przyjmuje postać |x² − 2x| ≥ x³, x∊(0,∞) |x|·|x − 2| ≥ x³, x∊(0,∞) |x − 2| ≥ x², x∊(0,∞) (dzielenie stronami przez x = |x| > 0 daje nierówność równoważną). Ostatnia nierówność jest równoważna alternatywie − x + 2 ≥ x², x∊(0, 2) lub x − 2 ≥ x², x∊<2,∞) 0 ≥ x²+x−2, x∊(0, 2) lub 0 ≥ x²−x+2, x∊<2,∞) Druga z tych nierówności nie ma rozwiązań, natomiast rozwiązaniami pierwszej są x∊<−1,1>∩(0,2) x∊(0,1> Odp. x∊(−∞,1>

J: @Aga1 .. x² − 2x − x³ ≥ 0 ⇔ x ∊ (−∞,0> x² − 2x + x³ ≤ 0 ⇔ x ∊ (−∞,−2> U <0,1> suma przedziałów: x ∊ (−∞,1> ( co jest zgodne z innymi rozwiązaniami)

Aga1.: @ J, wiem,że wyniki uzyskamy te same, bo sprawdziłam. Gdy mamy np. taką nierówność Ix²−2xI≥2 to x²−2x≥2 v x²−2x≤−2 natomiast Ix²−2xI≥x nie robiłabym w podobny sposób.

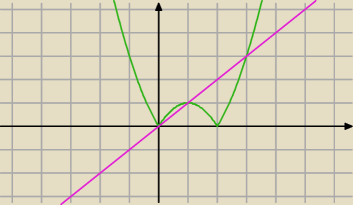
J: @Aga1 ... a dlaczego nie ? x² − 2x − x ≥ 0 ⇔ x ∊ (−∞,0] U [3,+∞] x² − 2x + x ≤ 0 ⇔ x ∊ [0,1] suma: x ∊ (−∞,1] U [3,+∞) .... i zgadza się

daras: a co na to ania

pigor: ..., zgodziłbym się z @Aga1 , bo przy rozwiązaniu analitycznym powinno się napisać, że |x²−2x| ≥ x ⇔ x< 0 v (x ≥0 i (x²−2x ≤ −x v x²−2x ≥ x)) ⇒ itd , czyli,dla x, x³, ..., xⁿ (n nieparzyste) po praw ej stronie daną nierówność spełnia każda liczba x< 0 i dopiero część wspólna z rozwiązaniem dla x ≥0 i (x²−2x ≤ −x v x²−2x ≥ x) daje poprawną końcową odpowiedź ...

pigor: ..., a propos ten przykład z x³ po prawej robiłem wczoraj tu : https://matematykaszkolna.pl/forum/301529.html ...

daras: ale tutaj nie ma archiwum uporządkowanego więc ten sam przykład można robić co tydzień, codziennie..w kółko

daras: z dowolną częstotliwością

pigor: ..., kurde; wróć do 14:17; nie "część wspólna", tylko ma być to "suma" ; przepraszam i ... znikam ...