Dowód rachunek prawdopodobirństwa gin: Udowodnij, że P(AUB) = P(A) + P(B) − P(ANB). Proszę o pomoc z tym dowodem

r: P(ANB) ?

gin: P(A iloczyn B)

kyrtap: po co udowadniać aksjomaty?

gin: No niestety musze to o udowodnić

5-latek: To zadzwon do Kolmogorowa

PW : Nie wszyscy to przyjmują jako aksjomat. Powołaj się na aksjomat o prawdopodobieństwie sumy zdarzeń rozłącznych dla zdarzeń rozłącznych (A\B∪B\A) i A∩B,

kyrtap: ja bym poszedł na łatwiznę i to zobrazował ^^ na dwóch rysunkach

gin: 5−latek, masz może jego numer?

gin: Muszę zrobić to w sposób od lewej do prawej

PW : Teraz kyrtap dobrze podpowiada: zobaczyć na rysunku to co sugeruję o 21:26 i zastosować aksjomat (dwa razy).

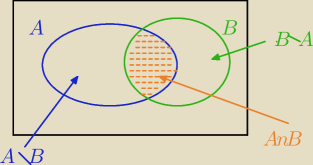
Mila: A∪B=(A\B)∪(A∩B)∪(B\A) Zbiory (A\B),(A∩B),(B\A) są rozłączne ⇔ P(A∪B)=P(A\B)+P(A∩B)+P(B\A)⇔ P(A∪B)=P(A)−P(A∩B)+P(A∩B)+P(B)−P(∩B)⇔ P(A∪B)=P(A)+P(B)−P(∩B)

kyrtap: Bardzo ładnie Mila

PW : Nie dała szansy ginowi, żeby to sam wymyślił . Jeszcze bym dodał, że dla rozłącznych A i B (tego rysunek nie obejmuje) twierdzenie jest oczywiste na mocy dwóch aksjomatów.

r: https://matematykaszkolna.pl/forum/301291.html