rozwiąż równanie bangrauhl: rozwiąż równanie metodą algebraiczną i graficzną : |x+1|=2−|x−1|

sushi_gg6397228: narysować umiesz lewą stronę ?

daras: https://matematykaszkolna.pl/strona/3410.html

daras: w poniedziałek nie mieli sushi dali mi kupon na 25 zet free

bangrauhl: narsować tak gorzej rozwiązać nie wiem jak zacząć

daras: https://matematykaszkolna.pl/strona/1653.html

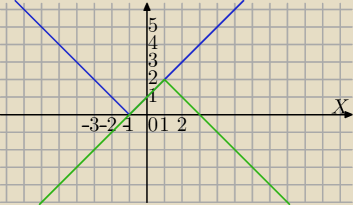
Mila: |x+1|=2−|x−1| Metoda graficzna: f(x)=|x+1| [Z[g(x)=2−|x−1| rozwiązanie : x∊<−1,1> Metoda algebraiczna: 1) |x+1|=x+1 dla x≥−1 |x−1|=x−1 dla x≥1 a) x<−1 −(x+1)=2−[−(x−1)]⇔ −x−1=2−(−x+1)⇔−x−1=x−1 −2x=0 x=0∉(−∞,−1) b) x∊<−1,1) x+1=2−(−x+1) x+1=2+x−1 1=1 prawda ⇔każda liczba x∊<−1,1) spełnia równanie c)x≥1 x+1=2−(x−1) x+1=2−x+1 2x=2 x=1∊<1,∞) Odp. x∊<−1,1>

PW : |x+1| + |x−1| = 2 Rozwiązanie graficzne to również interpretacja modułu różnicy dwóch liczb na osi. |x−1| to odległość liczby x od liczby 1, a |x+1| to odległość x od −1. Po narysowaniu na osi liczb −1 i 1 oraz gdzieś między nimi liczby x widać, że suma odległości równa jest 2, gdy x należy do odcinka <−1, 1>, i tylko wtedy.

pigor: ..., no właśnie, jestem za . ...