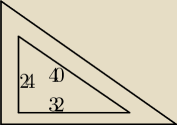
Zadanie Madzia: Bardzo proszę o pomoc Wokół klombu kwiatowego w kształcie trójkąta prostokątnego o wymiarach jak na rysunku, posiano trawę, tak, że szerokość trawnika wynosiła 2 m. Jaka jest powierzchnia gruntu obsianego trawą?

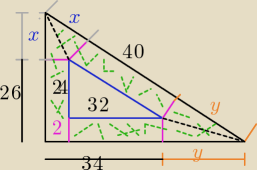
zefir: Podam rozwiązanie trójkąty są podobne więc: podstawa dużego: 32 +2+y = 34+y wysokość dużego: 24+2 +x = 26 +x przeciwprostokatna dużego: 40 +x +y

	34+y		32		4
to:		=		=
	26+x		24		3

	34+y		32		4
i		=		=
	40+x +y		40		5

102+3y = 104 +4x => −4x+ 3y = 2 i 170 +5y= 160 +4x +4y => 4x −y= 10 −−−−−−−−−−−− = 2y = 12 => y= 6m to x = 4m wymiary dużego trójkąta są podstawa = 40 m i wysokość 30m

	30*40
PD=		= 600m2
	2

	24*32
Pklombu =		= 384
	2

powierzchnia trawnika: 600m² − 384m²= 216m² Nie chce mi się już rysować nowego rysunku Może Bogdan narysuje < mruga> Witam Bogdanie

zefir:

BiebrzaFun : jak uzasadnić,że x lub y na przyprostokątnej jest równy x lub y na przeciwprostokątnej,czy na pewno przerywana linia dzieli kąty na połowę(to nie jest trójkąt równoramienny)? https://matematykaszkolna.pl/forum/29971.html w którym miejscu jest błąd w moim zamotanym rozwiązaniu,wyniki są zbliżone ,ale nierówne?

BiebrzaFun : Niestety zefirku,Twoje rozw. jest złe y=6 x=4 to a=30 b=42 c=50 30²+42²≠50² jeśli a²+b²=c² to (a+x)²+(b+y)²≠(c+x+y)²

Godzio: chyba źle dodałełeś bo boki są 40,30,50

BiebrzaFun : o tak ,faktycznie,przepraszam zefirka i za wprowadzenie w błąd.Godzio ,to gdzie tu jest błąd https://matematykaszkolna.pl/forum/29971.html