Znajdź wartość k KLAUDIA : Ustal dla jakich wartości parametru k dokładnie 4 liczby całkowite spełniają nierówność (x−1)(x−k)<0

Eta: k=−4 lub k=6

===: x²−kx−x+k<0 x²−(k+1)x+k<0 Δ=... x₁= x₂= i wszystko jasne

Eta: Gdzie jest warunek tylko "dodatnie" ? bo ja nie widzę?

ICSP: Moje oczy widzę dzisiaj więcej

Eta: Spryciarz IC.... ..

PW: Nierówność spełniają liczby zawarte w przedziale między 1 a k, tak więc dla k∊[1, ∞) rozwiązaniami są liczby x∊(1, k), a dla k∊(−∞, 1) są to liczby x∊(k, 1). Odpowiedz na pytanie: − Dla jakich wartości parametru k do przedziału (1, k) lub do przedziału (k, 1) należą dokładnie 4 liczby całkowite.

Antek: Eta, PW pomożecie https://matematykaszkolna.pl/forum/300701.html

KLAUDIA : a coś konkretniej? jak co po kolei?

prosta: przecież k nie musi być całkowite k>5 lub k<−3

PW : Zgadzam się z prostą, choć nie do końca. O 19:54 pisałem (wcale nie zakładając że k∊C): sprawdź 1 < n < k i sprawdź k < n < 1 − kiedy będą tylko cztery całkowite n?

Eta: Racja k nie musi być całkowite ( nie doczytałam

prosta: poprawka: −4≤<k<−3 lub 5 <k≤6

Eta: Dokładnie tak

prosta: ups...chyba przedziały długości 2 będą dobre: −5<k<−3 lub 5<k<6

prosta: mój ostatni post do usunięcia

KLAUDIA : nadal nwm jak to zrobić

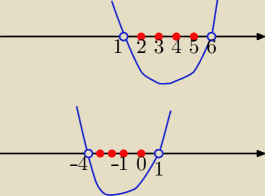
prosta: Rysunek u góry wyjaśnia sytuację opisaną w zadaniu. Rozwiązanie nierówności czytamy ze szkicu: miejsca zerowe to x₁=1, x₂=k.

prosta: 5<k≤6