odłegłość punktu
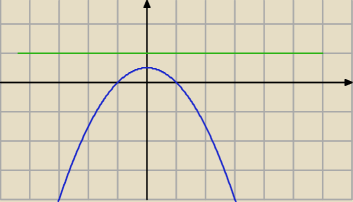
boom: znajdź zbiór punktów X leżących na płaszczyźnie R2 o własności: odległość punktu X od prostej
y=1 jest równa odległości X od punktu (0,0)
5 paź 22:02
Qulka:
5 paź 22:07
boom: a czy mogę prosić o wyjaśnienie?

5 paź 22:10
boom: jak wgl zabrać się za takie zadanie...
5 paź 22:10
5 paź 22:11
boom: te zależności znam, ale wciąż nie wiem od czego mam zacząć...
5 paź 22:15
pigor: ..., z warunków zadania
p{x2+y2= |y−1| /
2 ⇔ x
2+y
2= y
2+1−2y ⇔ 2y=−x
2+1 ⇔
⇔
y=12x2+12 − szukane miejsce geometryczne (parabola). ..

5 paź 22:15
pigor: ..., oczywiście
√x2+y2=|y−1| tam miało być. ...

5 paź 22:17
boom: chyba nadal nie rozumiem...

5 paź 22:19
Qulka: że odległość (x,y) od (0,0) /wzór z linku/ ma być równa odległości (x,y) od (x,1) /wzór z
linku/
5 paź 22:29
Bogdan:
Kiedyś w szkole średniej w ramach geometrii analitycznej podawane były definicje paraboli,
elipsy, hiperboli. Tamtejszy uczeń na pytanie zawarte w podanym tu zadaniu od razu
udzieliłby poprawnej odpowiedzi. Dzisiaj nie omawia się tych zagadnień i stąd boom
ma problem.
Zbiór punktów płaszczyzny równo oddalonych jednocześnie od danej prostej i danego punktu
nie należącego do tej prostej to parabola.
Tę prostą nazywamy kierownicą paraboli, a dany punkt − ogniskiem paraboli.
5 paź 22:34
pigor: ...,
niech P=(x,y) dowolny punkt szukanego zbioru punktów
spełniających warunki zadania i O= (0,0) − początek układu XOY
to ich odległość |PO|=
√(0−x)2+(0−y)2=
√x2+y2 − moja lewa strona równania
jednocześnie ten punkt P=(x,y) jest odległy od prostej y=1 ⇔ 0x+1y−1=0 :
o wielkość |y−1| co jest oczywiste, albo z wzoru na odlegośc punktu od prostej :
| | |0x+1y−1| | | |y−1| | |
d= |
| = |
| = |y−1|, no i masz moje równanie |
| | √02+12 | | √1 | |
które po przekształceniu u mnie jak wyżej jest równaniem paraboli, czyli
zbioru szukanych punktów (x,y) paraboli
y= 22x2+12 i tyle...

5 paź 22:41
Qulka: ale na logikę powinna być wersja minus

5 paź 22:43
Mila:
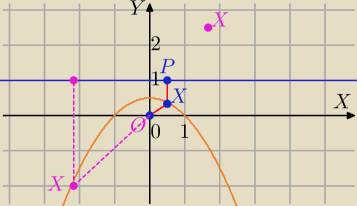
1) Dla X(x,y) leżących nad prostą y=1 odległość Punktu X od prostej jest mniejsza niż |OX|.
2) Rozważymy punkty X(x,y) gdzie y<1
|PX|=|OX|
X=(x,y)
P=(x,1)
O=(0,0)
|PX|=
√(x−x)2+(y−1)2
|OX|=
√(x2+y2
√(y−1)2=
√x2+y2
y
2−2y+1=x
2+y
2
−2y=x
2−1
5 paź 22:52
Mila:
22:15 Pigor zgubił (−)
5 paź 22:57
pigor: ..., przepraszam, tak

w poście z godziny 22:15
mój błąd nieuwagi ; "zjadłem" znak minus (−). ...

5 paź 23:05
boom: pigor, nie rozumiem 4 linijki z postu o godz 22:41

5 paź 23:54
boom: ale zrozumiałam rozwiązanie Mili

DZIĘKUJĘ WAM WSZYSTKIM BAAARDZO

6 paź 00:01







 1) Dla X(x,y) leżących nad prostą y=1 odległość Punktu X od prostej jest mniejsza niż |OX|.
2) Rozważymy punkty X(x,y) gdzie y<1
|PX|=|OX|
X=(x,y)
P=(x,1)
O=(0,0)
|PX|=√(x−x)2+(y−1)2
|OX|=√(x2+y2
√(y−1)2=√x2+y2
y2−2y+1=x2+y2
−2y=x2−1
1) Dla X(x,y) leżących nad prostą y=1 odległość Punktu X od prostej jest mniejsza niż |OX|.
2) Rozważymy punkty X(x,y) gdzie y<1
|PX|=|OX|
X=(x,y)
P=(x,1)
O=(0,0)
|PX|=√(x−x)2+(y−1)2
|OX|=√(x2+y2
√(y−1)2=√x2+y2
y2−2y+1=x2+y2
−2y=x2−1
 w poście z godziny 22:15
mój błąd nieuwagi ; "zjadłem" znak minus (−). ...
w poście z godziny 22:15
mój błąd nieuwagi ; "zjadłem" znak minus (−). ...

 DZIĘKUJĘ WAM WSZYSTKIM BAAARDZO
DZIĘKUJĘ WAM WSZYSTKIM BAAARDZO 