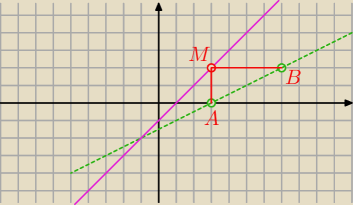
Dane są punkty hihihi: Dane są punkty A = (3,0) i B = (7,2). Na prostej o równaniu x – y – 1 = 0 wyznacz taki punkt, aby |<AMB|=90st

Mila: Tam masz podobne zadanie, https://matematykaszkolna.pl/forum/300506.html

hihihi: no to niestety zupełnie inne zadanie, takie które jest w linku, jest proste, a tutaj proste się nie przecinają niestety

Mila: Nie przeczytałaś uważnie. Po kolacji napiszę.

===:

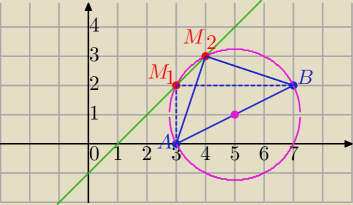
Mila: |∡AMB|=90⁰ ⇔ΔABM jest trójkątem prostokątnym, a odcinek AB jest przeciwprostokątną. x – y – 1 = 0 ⇔y=x−1

	3+7		0+2
S=(		,		)=(5,1)
	2		2

Kreślimy okrąg o środku S(5,1) i promieniu r=√2²+1²=√5 Równanie okręgu: (x−5)²+(y−1)²=5 Punkt przecięcia prostej i okręgu: (x−5)²+(x−1−1)²=5⇔ (x−5)²+(x−2)²=5 x²−10x+25+x²−4x+4=5 2x²−14x+24=0 /:2 x²−7x+12=0 Δ=49−48=1 Będą dwa punkty przecięcia

	7−1
x1=		=3 wtedy y=3−1=2⇔ M1=(3,2)
	2

	7+1
x2=		=4 wtedy y2=3 ⇔ M2=(4,3)
	2

|∡AM₁B|=90⁰ jako kąt wpisany w okrąg oparty na średnicy |∡AM₂B|=90⁰ jako kąt wpisany w okrąg oparty na średnicy Drugi sposób z iloczynu skalarnego wektorów.

===:

Mila: Jakoś nie spieszy się autorka do zadania.

hihihi: czemu uważasz że się nie spiesze próbuje je zrobić, razem z tym co mi tutaj umieściliście, żeby to zrozumieć Mi chodzi o to żeby zrozumieć, a nie spisać gotowca Dziękuję za rozwiązanie i pomoc

Mila: No i co rozumiesz?

hihihi: Tak Dziękuje

Mila: Proszę

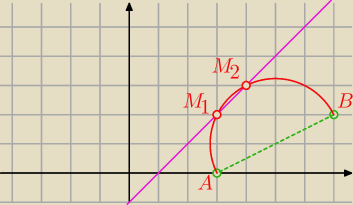
pigor: ..., dane są punkty A = (3,0) i B = (7,2). Na prostej x–y–1= 0 wyznacz taki punkt M, aby |<AMB|=90^o. −−−−−−−−−−−−−−−−−−−−−−−−−−− M patrz i myśl , bo inaczej z iloczynu skalarnego wektorów np. tak: niech M=(x,y)= (x, x−1)=?, to MA^→= [3−x,0−y] i MB^→= [7−x,2−y] , zatem |∡AMB|= 90^o ⇔ MA^→⊥ MB^→ ⇔ [3−x, −x+1] ◯ [7−x, 2−x+1]= 0 ⇔ ⇔ (3−x)(7−x)+(1−x)(3−x)= 0 ⇔ 21−10x+x² + 3−4x+x²= 0 ⇔ 2x²−14x+24=0 ⇔ ⇔ x²−7x+12= 0 ⇔ x=3 v x=4 ⇒ M=(3,2) v M=(4,3) .

hihihi: Dziękuje wszystkim Jesteście niezwykle pomocni Zrozumiałam wszystko