Różnowartościowość Dominik:

	1
Jak uzasadnić że funkcja f(x)=x−√x jest różnowartościowa na zbiorze <		;∞) ?
	4

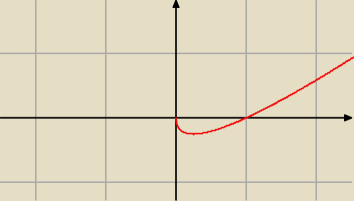
Janek191: f(x) = x − √x ; x ≥ 0

	1		1
f '(x) = 1 −		= 0 ⇔ 2√x = 1 ⇔ x =
	2√x		4

	1		1
f ' zmienia znak z − na + w x =		, zatem w x =		funkcja f ma
	4		4

minimum lokalne.

	1
f rośnie w <		; +∞ ), więc jest różnowartościowa.
	4

Janek191: f(x) = x − √x ; x ≥ 0

	1		1
f '(x) = 1 −		= 0 ⇔ 2√x = 1 ⇔ x =
	2√x		4

	1		1
f ' zmienia znak z − na + w x =		, zatem w x =		funkcja f ma
	4		4

minimum.

	1
f rośnie w <		; +∞ ), więc jest różnowartościowa.
	4

Janek191: f(x) = x − √x ; x ≥ 0

	1		1
f '(x) = 1 −		= 0 ⇔ 2√x = 1 ⇔ x =
	2√x		4

	1		1
f ' zmienia znak z − na + w x =		, zatem w x =		funkcja f ma
	4		4

minimum.

	1
f rośnie w <		; +∞ ), więc jest różnowartościowa.
	4

Janek191: Coś mi wariuje Internet

Dominik: Dzięki a bez pochodnej da się takie zadanie rozwiązać? Pytam tak dla własnej informacji?

PW: Uzasadnienie ma być "z definicji", czy można posługując się pochodną? Dobrze jest pisać na jakim poziomie oczekujesz rozwiązania.

PW: Zanim zapytałem, to Janek191 już rozwiązał. Da się i bez pochodnej.

Dominik: No właśnie wolał bym z definicji.

Dominik: A podpowiedział byś jak zrobić to z definicji?

Nuti: Z definicji (że funkcja jest różnowartościowa w przedziale wtedy i tylko wtedy gdy równość jej wartości na argumentach z tego przedziału implikuje równość tych argumentów): Można na przykład pokazać, że jeżeli dla pewnych dodatnich x i z (w zasadzie powinnam pisać x₁ i x₂, bo taka jest konwencja oznaczania dwóch różnych elementów dziedziny, ale nie chce mi

	1
się pisać indeksów...) z przedziału <		,∞) zachodzi x−√x=z−√z, to x=y.
	4

	1
Załóżmy więc, że istnieją w <		,∞) takie x i z, że x≠z i x−√x=z−√z.
	4

Wówczas x−z=√x−√z (rozszerzamy prawą stronę do ułamka domnażając przez sprzężoną)

	x−z
x−z=		(dzielimy obie strony przez x−z, bo jest różne od 0)
	√x+√z

√x+√z=1

	1
a to oznacza, ze względu na dodatniość obu liczb, że musi zachodzić √x∊(0,		) lub
	2

	1		1		1
√z∊(0,		)a więc x∊(0,		) lub z∊(0,		), co jest sprzeczne z założeniem.
	2		4		4

Musiało więc zachodzić x=z.

Nuti: w piątej linii napisałam pomyłkowo x=y zamiast x=z.

5-latek: Dzien dobry Nuti Spojrzysz na moje ? https://matematykaszkolna.pl/forum/299526.html

Nuti: Cześć @5−latek Chętnie spojrzę, ale ja się do bólu nie znam na przybliżeniach...

5-latek: To tak jak ja Mam jeszcze kilka zadań z tego dzialu

Nuti: Współczuję...

5-latek: Dziekuje CI bardzo za wspolczucie To jest dopiero 1 klasa , a co będzie do 4 klasy ? Wole nie myslec

Nuti: Co to za szkoła, tzn. jaki rodzaj szkoły?

5-latek: Pani przedszkolanka powiedziała ze już za długo jestem w przedszkolu i czas isc do 1 klasy

Nuti: Racja, co za długo, to niezdrowo.

5-latek: A powiem CI ze nie wiem czy się nia zalamie Bo patrze na spis do książki i mamy 1)Liczby rzeczywiste 2)Funkcje 3)Figury geometryczne 4)Rownania i nierownosci 5) Przeksztalcenia geometryczne 6)Jednokladnosc i podobieństwo 7)Funkcje trygonometryczne A tak dobrze miałem w przedszkolu ,no ale Pani się uparla i nie ma odwołania

5-latek: Pewnie wiesz ze sobie zartuje . Oczywiście 1 klasa liceum

Nuti: Musisz czy chcesz?

5-latek: Tak poważnie W moim przypadku bardziej chciejstwo niż mus

Nuti: A, to dobrze, bo nie umiałam rozwiązać Twojego zadania

5-latek: NIc nie szkodzi Może jak wroce z pracy kolo 23 i będzie Mila na forum to ja poproszse . Ona ma ta ksiazke (Anusiak 1 klasa liceum 1993r

Nuti: Powodzenia! Ja tu nie mam żadnego podręcznika, a w tym przypadku to naprawdę potrzebne.

5-latek: