Obliczyć pole ograniczone wykresami funkcji Amor: Obliczyć pole ograniczone wykresami funkcji : f(x) = 2x² − 5x i g(x) =x² − 3x

Nuti: Policz punkty przecięcia krzywych, a pole obszaru wyraża się całką od x−owej lewego punktu przecięcia do x−owej prawego z różnicy wartości twoich funkcji. Całka super łatwa. Będzie Ok?

Amor: @Nuti jakbym wiedział jak to obliczyć to nie prosiłbym o rozwiązanie

daras: to zacznij coś robić https://matematykaszkolna.pl/forum/121854.html

Nuti: Narysuj sobie obie krzywe, są naprawdę łatwe do narysowania. f(x): f(x)=2x²−5x=x(2x−5)

	5
czyli miejsca zerowe są 0 i		. Ramiona paraboli w górę, bo współczynnik przy x2 dodatni.
	2

	5		1
Jeżeli chcesz narysować dokładnie, oblicz wierzchołek paraboli (		,−3		).
	4		4

g(x): g(x)=x²−3x=x(x−3)

	3		1
czyli miejsca zerowe są 0 i 3. Ramiona w górę, wierzchołek (		,−2		).
	2		4

Punkty przecięcia krzywych: f(x)=g(x) 2x²−5x=x²−3x x²−2x=0 x(x−2)=0 Krzywe przecinają się w x równych 0 i 2. Pole między krzywymi to całka od 0 do 2 z (x²−3x)−(2x²−5x)=−x²+2x Umiesz ją policzyć?

5-latek: Niech kolega się dobrze zastanowi nad swoimi dalszymi studiami jeśli nie potrafi rozwiazac prostego równania 2x²−5x=x²−3x

Nuti: źle podałam wierzchołek pierwszej paraboli (to dla twojego rozwiązania kompletnie bez

	1
znaczenia, ale na wszelki wypadek zgłaszam gdybyś się zastanawiał): powinno być −3		.
	8

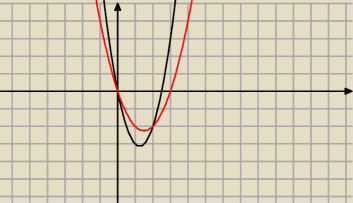
5-latek: czarna y=2x²−5x ,czerwona y=x²−3x

Kacper: Student nieumiejący narysować paraboli?

5-latek : Witaj Kacper Dlaczego nie dajesz wiary ?

Kacper: Dobry 5−latek czasem ręce opadają, jak widzisz, że ktoś dostał się na studia, a najprostszych rzeczy nie umie.

5-latek : Wiesz ja czasami tez nie dowierzam .

henrys: Cześć, fakt problem w tym, czy pisać rozwiązania i utwierdzać w przekonaniu, że ten ktoś umie (tylko ma niewielkie zaległości, które przecież są tak niewielkie, że jak mu się tylko będzie chciało to migiem nadrobi)

5-latek : Witaj Nie wiem czy pamietasz to rownanie ktore kiedys rozwiazywalismy ? Mila tez twierdzi ze dla n parzystego sa dwa rozwiazania

henrys: i ma rację

5-latek : Po niedzieli wstawie nowe .

J: Witam Panów ...jest jeszcze gorzej, bo kolega/koleżanka Amor ma jeszcze równanie różniczkowe do rozwiązania

5-latek: Witaj J Chyba ma poprawke