suriekcja,bijekcja, iniekcja kamil: Czy mógłby ktoś po chłopsku wytłumaczyć suriekcję,bijekcję i iniekcję? Na razie rozumiem to tak: suriekcja − wszystkie elementy przeciwdziedziny musza przyjmować jeden lub więcej argumentów. Przeciw dziedzina musi być równa argumentowi? iniekcja − funkcja różnowartościowa. Jest to funkcja, która dla różnych argumentów przyjmuje różne wartości. Więc argument nie może być równy przeciwdziedzinie? Przeciwdziedzina może nie zawierać żadnego argumentu? bijekcja − iniekcja i suriekcja w jednym. Czyli wszystkie elementy przeciwdziedziny muszą zawierać po jednym argumencie nie równym przeciwdziedzinie?

PW: Słowa "przeciwdziedzina" używasz w niewłaściwym znaczeniu. Jeszcze raz przeczytaj na spokojnie definicje (łącznie z definicją przeciwdziedziny).

Nuti: @PW ma rację. Krótko: surjekcja − funkcja „na" jakiś zbiór, czyli każdy element z tego zbioru jest wartością tej funkcji dla jakiegoś argumentu. injekcja − funkcja różnowartościowa, czyli żaden element z przeciwdziedziny nie jest wartością funkcji dla dwóch różnych elementów. bijekcja − różnowartościowa i na. Ma to sens jedynie, gdy mówisz konkretnie o funkcji f:X−−−>Y (wyraźnie określasz dziedzinę i przeciwdziedzinę). Na przykład sin:(−Pi/2,Pi/2)−−−>(−1,1) jest bijekcją, ale sin:R−−−>R nie.

Nuti: ja tak po babsku wytłumaczyłam

henrys:

Janek191: Najlepsze są grafy

Nuti: @Janek191 Explain, please!

kamil: to jak wyznaczać ilość suriekcji,bijekcji i iniekcji? https://matematykaszkolna.pl/forum/298646.html

kamil: mógłby ktoś to suriekcję i iniekcję pokazać na rysunku? Bo nadal nie mogę tego zrozumieć.

kamil: jak dla mnie bijekcja to to samo co iniekcja. Bo iniekcja od suriekcji różni się tylko tym, że zbiór B może zawierać tylko jeden argument zbioru A, gdzie suriekcja mogła zawierać ich kilka.

Nuti: Spójrz na te funkcje: sin:R−−−>R nie jest ani injekcja ani surjekcja sin:R−−−>[−1,1] jest surjekcja ale nie injekcja sin: [−Pi/2,Pi/2]−−−>[−1,1] jest i surjekcja i injekcja Kapisz?

kamil: nie. chyba suriekcję już w miare rozumiem, ale iniekcję nie.

Nuti: sin: [−Pi/2,Pi/2]−−−> R jest injekcja, ale nie jest surjekcja, wiec nie jest bijekcja!

Nuti: Injekcja to po prostu różnowartościowa, ale nie musi być koniecznie NA cały zbiór (patrz ostatni przykład)

kamil: możesz podać inny przykład bez sinusów?

Nuti: Wszystko zależy od tego, skąd dokąd definiujemy funkcję

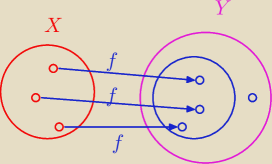
Janek191: w Iniekcja f : X → Y, czyli funkcja ze zbioru X w zbiór Y

kamil: ale w iniekcji zbiór B może zawierać tylko jeden element ze zbioru A? w suriekcji zbiór B może zawierać kilka argumentów ze zbioru A?

Nuti: Kurde, sinus jest najwdzięczniejszy... Co ci się nie podoba w sinusie?

kamil: ale te jedno kółko nie połączone niebieskie też należy do zbioru wartości. W suriekcji byłoby połączone, a w iniekcji już nie?

Nuti: @Janek191 Ładnie!

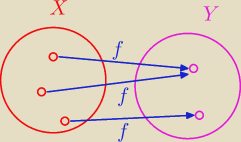
Janek191: na Suriekcja f : X → Y , czyli funkcja ze zbioru X na cały zbiór Y

Nuti: @kamil surjekcja nie jest jakimś przeciwieństwem injekcji... To są dwie cechy niezależne od siebie.

kamil: ok dzięki za rysunki lecz teraz nie rozumiem tej bijekcji. Bo jeśli to jest suriekcja i iniekcja razem to kilka argumentów może zawierać tą samo wartość?

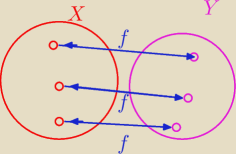
Janek191: Bijekcja f : X → Y , czyli funkcja "na" i różnowartościowa ≈ Y = f( X)

kamil: ale skąd te strzałki w lewo?

Janek191: Bo jest to funkcja wzajemnie jednoznaczna . ← to f⁻¹

kamil: iniekcja z tego co wyczytałem jest też jednoznacza, czyli w dwie strony działa?

Nuti: @kamil Nie. Surjekcja i injekcja są to cechy kompletnie od siebie niezależne. Surjekcja mówi tyle, że wszystkie elementy zbioru Y są wykorzystane jako wartości funkcji, ale nie wypowiada się na temat, czy coś jest użyte jako wartość raz czy więcej razy. To nie jest zadanie surjekcji. Injekcja z kolei ma to w d...e, czy każdy element ze zbioru Y jest użyty jako wartość czy nie, dla niej liczy się tylko to, że jeżeli coś już jest wartością, to jest nią tylko raz, czyli dla jednego argumentu. Bijekcja z kolei troszczy się i o jedno i o drugie. Czyli każdy element musi być wartością dla jakiegoś argumentu i to tylko dla jednego. Jasne?

kamil: aha czyli w bijekcji nie może być wolnych elementów w zbiorze Y tak jak w iniekcji? Chyba w końcu zrozumiałem.

Janek191: Iniekcja nie działa na cały Y , więc nie istnieje f⁻¹ od argumentu ( kółeczko poza niebieskim zbiorem) na I grafie.

Nuti: TAK!

kamil: ok dzięki za te tłumaczenia

Nuti: To znaczy w injekcji MOGą być wolne elementy w Y, ale nie muszą. A w surjekcji (a w szczególności w bijekcji, która jest z definicji również surjekcją) NIE MOŻE ich być.

kamil: a czy mógłby ktoś wyjaśnić jak się liczy liczbę iniekcji,suriekcji i bijekcji z określonych zbiorów?

b.: Może dodam taką jedną rzecz. Formalnie biorąc, jak się ma jakąś funkcję, to ma ona jakąś dziedzinę i przeciwdziedzinę. Można (hmm może trochę niepoprawnie) myśleć, że funkcja to taka trójka: (dziedzina, przeciwdziedzina, przyporządkowanie elementom dziedziny elementów przeciwdziedziny) Czyli np. f:R−>R dana wzorem f(x)=x² g:R−>[0,∞) dana wzorem g(x)=x² to różne funkcje. Często chyba myśli się o funkcji tylko jako o przyporządkowaniu −− i jak się tak myśli, to trudno zrozumieć definicje z pierwszego posta.

Nuti: A, to ty cały czas o zbiorach skończonych! To rozumiem twoją niechęć do sinusa! Ale pojęcia są na szczęście takie same w przypadku zbiorów skończonych i nieskończonych.

Nuti: @b ja to już tłumaczyłam na przykładzie sinusa, ale okazuje się, że Kamilowi chodzi o funkcje na zbiorach skończonych.

b.: @Nuti: widziałem, że tłumaczyłaś, ale miałem wrażenie, że nie dotarło

Nuti: @kamil Ilość bijekcji − bijekcja może istnieć oczywiście tylko między zbiorami równolicznymi. Gdy X i Y mają po n elementów, to bijekcji z X do Y jest tyle ile permutacji zbioru n−elementowego, czyli n! (pomyśl o tym tak − każda funkcja to inne ustawienie elementów zbioru Y). Niech ktoś to potwierdzi, bo już jestem śpiąca i może głupoty gadam...

b.: @Nuti: potwierdzam

kamil: a jak z suriekcją i iniekcją ? jak je wyznaczać?

Nuti: @b dzięki! Zwijam interes na dzisiaj

Nuti: @kamil kombinatoryka, ale mi już mózg wysiadł na dzisiaj. Dobranoc!

Nuti: @kamil Już wszystko wiesz na ten temat? Widziałam, że umieściłeś dodatkowe zadanie, o liczbie injekcji. Ogólnie − przypomnij sobie podstawy kombinatoryki.

Nuti: Przy okazji zwrócę uwagę, że wczoraj wieczorem użyłam niewłaściwego słowa pisząc „ilość bijekcji". Powinno być „liczba bijekcji", bo słówka „ilość" używa się do niepoliczalnych (woda, cukier,...). Jest więc liczba drzew w lesie, liczba dzieci itd.

kamil: iniekcja − funkcja różnowartościowa. Jest to funkcja, która dla różnych argumentów przyjmuje różne wartości. Czy takie tłumaczenie jest ok?

J: W uproszczeniu ..tak. ZFormalna definicja : ∀ x₁,x₂ ∊ D : x₁ ≠ x₂ f(x₁) ≠ f(x₂)

kamil: a jak dla suriekcji i bijekcji formalna definicja wygląda?

J: Suriekcja: ∀ y ∊ Y ∃ x ∊ X : f(x) = y Bijekcja: Funkcja jest bijekcją,jeśli jest suriekcją i iniekcją.

b.: @11:02: zabrakło implikacji => w definicji, powinno być x₁≠x₂ => f(x₁) ≠ f(x₂)