trapez
Eta: Dany jest trapez ABCD o podstawach AB∥CD
Punkty E i F są odpowiednio środkami przekątnych AC i BD.
Wykaż ,że jeżeli |∡ABE|=|∡DBC| to |∡ACD|=|∡BCF|

28 sie 17:35
Eta: Nikt się nie skusi ? ..............

28 sie 19:10
Mila:
Ostatnie dni wakacji i uczniowie balują.
28 sie 19:14
Eta:
Hej
Mila 
28 sie 19:24
Mila:

Witam ciepło (29
0C).
28 sie 19:29
Eta:
@
anaisy
zadanko dla Ciebie

28 sie 20:20
Eta:
Hej
Kacper może Ty się skusisz?

28 sie 20:24
Kacper:
Eta 
Zaraz zrobię rysunek

Dzisiaj się trochę przeprowadzałem i zmęczony jestem, ale zerknę
28 sie 20:31
Kacper:
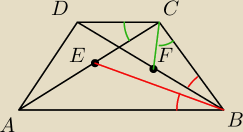
Mam rozumieć, że taka treść zadania?

28 sie 20:37
Eta:
Dokładnie tak

28 sie 20:55
Kacper:
Dzisiaj idę spać

Być może zwykłe liczenie kątów załatwi sprawę, ale biorąc pod uwagę fakt, że E i F to środki
zapewne trzeba będzie jeszcze coś "zobaczyć"

28 sie 20:58
Eta:
Choć ten rys. (wyszedł Ci "koślawo"

28 sie 20:58
Eta:
Ok ..... odpoczywaj

28 sie 20:59
Kacper:
Muszę przyznać, że teraz am trochę czasu i

i

i chyba pustka. Tragedia

29 sie 18:02
Mila:
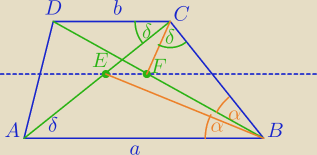
29 sie 18:28
Kacper:
Ładniejszy rysunek

29 sie 18:53
henrys: Ładne zadanie, żeby dowiedzieć się co to jest symediana (bez tej wiedzy też rozwiązywalne

)
29 sie 18:59
Eta: 
29 sie 21:55
Metis: Dwa razy Pitagoras'em

29 sie 21:59
29 sie 22:04
29 sie 23:02
Kacper:
Metis pochwal się zatem

30 sie 14:25
Eta:
A ja wciąż czekam na ten dowód

30 sie 14:28
Eta:
@
Kacper
podpowiedź .... "coś dorysować" i .....

30 sie 14:30
Kacper:
Jak zwykle "coś" dorysowujemy

30 sie 14:31
Eta: 
30 sie 14:32
Kacper:
Jednak będę musiał się udać po okulary. Geometrii chyba nigdy nie opanuje na zadowalającym mnie
poziomie

A niestety uczniowie czekać na to nie będą

30 sie 14:37
Eta:
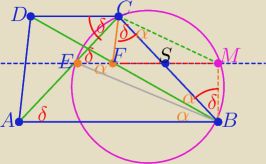
Wykreślamy równoległobok BFCM ( M symetryczny do F względem S)
|∡BCM|=|∡DBC|=|∡BEM|=α ⇒ punkty B,E,C,M leżą na jednym okręgu
bo |∡BEC|=α+δ i |∡BMC|= 180
o−(α+δ)
zatem: |∡ACD|=|∡CEM|=|∡CBM|=|∡BCF| =
δ
c.n.w

30 sie 16:23
Metis: 
30 sie 17:39
Kacper:
Metis co z twoim rozwiązaniem?

30 sie 18:04



 Witam ciepło (290C).
Witam ciepło (290C).


 Zaraz zrobię rysunek
Zaraz zrobię rysunek  Dzisiaj się trochę przeprowadzałem i zmęczony jestem, ale zerknę
Dzisiaj się trochę przeprowadzałem i zmęczony jestem, ale zerknę
 Mam rozumieć, że taka treść zadania?
Mam rozumieć, że taka treść zadania? 

 Być może zwykłe liczenie kątów załatwi sprawę, ale biorąc pod uwagę fakt, że E i F to środki
zapewne trzeba będzie jeszcze coś "zobaczyć"
Być może zwykłe liczenie kątów załatwi sprawę, ale biorąc pod uwagę fakt, że E i F to środki
zapewne trzeba będzie jeszcze coś "zobaczyć" 


 i
i  i chyba pustka. Tragedia
i chyba pustka. Tragedia 


 )
)







 A niestety uczniowie czekać na to nie będą
A niestety uczniowie czekać na to nie będą 
 Wykreślamy równoległobok BFCM ( M symetryczny do F względem S)
|∡BCM|=|∡DBC|=|∡BEM|=α ⇒ punkty B,E,C,M leżą na jednym okręgu
bo |∡BEC|=α+δ i |∡BMC|= 180o−(α+δ)
zatem: |∡ACD|=|∡CEM|=|∡CBM|=|∡BCF| =δ
c.n.w
Wykreślamy równoległobok BFCM ( M symetryczny do F względem S)
|∡BCM|=|∡DBC|=|∡BEM|=α ⇒ punkty B,E,C,M leżą na jednym okręgu
bo |∡BEC|=α+δ i |∡BMC|= 180o−(α+δ)
zatem: |∡ACD|=|∡CEM|=|∡CBM|=|∡BCF| =δ
c.n.w


