w oczekiwaniu na wyniki maturzysta: Kiedy pojawi się dzisiejszy arkusz matruralny z rozwiązaniami ?

Kacper: CKE nie chciałoby, żeby w ogóle się nie pojawił

maturzysta: jak to ? dlaczego?

Mila: Tu masz linka https://matematykaszkolna.pl/forum/297927.html

maturzysta: dzięki , a rozwiązania ? najlepiej z wytlumaczeniem?

Mila: Tam masz część zadań z odpowiedziami i niektóre rozwiązane. Pisz problemy.

Mila: .pl/edulandia/56,118533,18625575,matura−poprawkowa−2015−z−matematyki−poziom− podstawowy−publikujemy.html

Mila: na początku www.edulandia.pl dalej widać.

Eta: http://www.echodnia.eu/apps/pbcs.dll/article?AID=/20150825/EDUKACJA/150829476

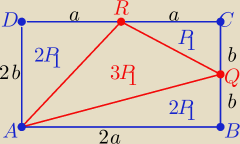
Eta: zad.31/

	1
P(CQR)=		ab= P1 , P(ADR)=P(ABQ)=ab = 2P1
	2

P(ABCD)=4ab= 8P₁ P(AQR)= 8P₁−5P₁= 3P₁= P(ADR)+P(CQR) c.n.u

prosta: zad.30/ x³+y³≥x²y+xy² (x+y)(x²−xy+y²)≥xy(x+y) (x+y)(x²−2xy+y²)≥0 (x+y)(x−y)²≥0 x+y≥0 dla x≥0 i y≥0 (x−y)²≥0 dla dowolnego x,y

Eta:

Eta: zad.29/ Kąt α jest ostry i spełnia równość:

	1		7
tgα+		=		Oblicz wartość wyrażenia sinα*cosα
	tgα		2

sinα		cosα		7
	+		=
cosα		sinα		2

sin2α+cos2α		7		2
	=		⇒ ..... sinα*cosα=
sinα*cosα		2		7

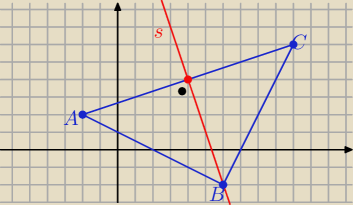
Eta: zad.32/ A(−2,2) , B(6,−2), C(10,6) trójkąt ABC jest równoramienny o ramionach |AB|=|BC|=√8²+4²=√80=4√5 zatem oś symetrii tego trójkąta jest prostą zawierającą wysokość opuszczoną z wierzchołka B na podstawę AC

	yC−yA		1
wsp. kierunkowy aAC=		=...=
	xC−xA		3

to oś symetrii s trójkąta ma równanie: s : y= −3(x−x_B)+y_B ⇒ y= −3x+16

Eta: zad.34/ f(x)=ax²+bx+c f(x)>0 ⇔ x∊(0,12) ⇒ parabola skierowana ramionami do dołu i miejsca zerowe f(x) to : x=0 v x=12

	0+12
funkcja w postaci iloczynowej : f(x)= ax(x−12) i xw=		=6
	2

f(x)osiąga największą wartość równą 9 ⇒ f(6)=9

	1
to 9=a*6(6−12) ⇒ ......... a= −
	4

f(x)=ax²−12ax ⇒ b=−12a= 3 i c=0 odp: a= −¹₄, b= 3, c=0

Mila: Witaj pracowita pszczółko. Też mam takie wyniki. Jaki wynik masz w (33) . Nie chce mi się dwa razy liczyć.

	640√3
V=		?
	3

Eta: Hej Mila zad 33/ wynik ok

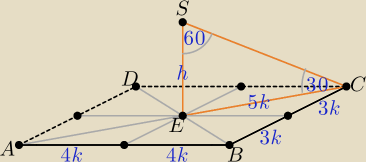
Bogdan: Można zadanie 33 tak rozwiązać. k > 0, 8k * 6k = 192 ⇒ k² = 4 ⇒ k = 2,

	√3
|EC| = √9k2 + 16k2 = 5k = 10 h = |EC|*tg30o = 10*
	3

	1		√3		640√3
Objętość V =		*192*10*		=
	3		3		3

Eta:

Bogdan: Zadanie 34 można rozwiązać z zastosowaniem wzorów Viete'a (pod warunkiem, że poprawkowicz poznał te wzory). x₁ = 0, x₂ = 12, x_w = 6, y_w = 9 c = a*x₁*x₂ = a*0*12 = 0, b = −a(x₁ + x₂) = −a*(0 + 12) = −12a f(6) = 9 ⇒ a*6² + b*6 + c = 9 ⇒ 36a − 72a = 9

	9		1		1
a = −		= −		, b = −12*(−		) = 3, c = 0
	36		4		4

Mila: Dobranoc

Bogdan: Dobranoc

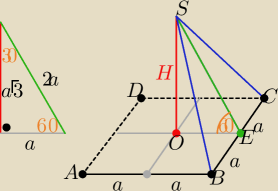
Eta: Na dobranoc zad.34 (5pkt ( stara matura) poprawkowa W ostrosłupie prawidłowym czworokątnym ściana boczna o polu 10 jest nachylona do płaszczyzny podstawy pod kątem 60^o. Oblicz objętość ostrosłupa.

	1
P(BCS)=		*2a*2a ⇒ 2a2 =10 ⇒ a=√5 ,Pp=4a2=20, H=a√3=√15
	2

	1		20√15
V=		Pp*H ⇒ V=		[j3]
	3		3

Miłych snów