matematykaszkolna.pl
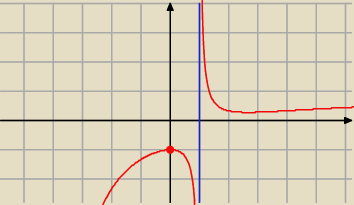
Pochodne Paula: wyznacz przedział monotoniczności f(x)=x2−3x+4x2+3x−4 pochodna wyszła mi f'(x)=6x2−8x+24(x2+3x−4)2 Nie wiem co dalej, tzn. nie potrafię wyznaczyć x0, ogólną zasadę wyznaczania znam
22 sie 15:08
Paula: f(x)=x2−3x+4/x2+3x−4 f ' (x)=6x2−8x+24/(x2+3x−4)2 może będzie czytelniej
22 sie 15:10
daras: a co to jest xo ?
22 sie 15:37
Ksekse: miejsce zerowe, czyli punkt, w którym wykres przecina się z osią OX, potrzebne do obliczenia
22 sie 15:41
Paula: dokładnie emotka
22 sie 15:42
daras: musisz jeszcze popracować nad liczeniem pochodnej, bo masz źle
22 sie 15:46
daras: a jak już poprawisz to liczysz prosta nierówność kwadratową: https://matematykaszkolna.pl/strona/93.html
22 sie 15:48
daras: nierówność jest jeszcze prostsza, liniowa na pewno dasz radę emotka
22 sie 15:51
Paula: pochodna wyjdzie 6x2−16x/(x2+3x−4)2?
22 sie 17:12
Paula: nie wiem już, dobrze czy źle, ktoś zerknie?
22 sie 17:25
henrys: źle obliczyłaś pochodną
22 sie 17:27
henrys: a teraz ok emotka
22 sie 17:27
Paula: Ale nadal jest coś źle, bo: przyrównuje górę do zera: 6x2−16x=0 x=0 v x=8/3 v x=−8/3 przedziały monotoniczności wychodzą: f rośnie w przedziałach (−8/3;0); (8/3;+ nieskończoności ) f maleje w przedziałach (−nieskoń.;−8/3); (0:8/3) tymczasem w książce jest odpowiedź; rośnie w (−nieskoń:−4), (−4;0)8/3;+nieskoń) a maleje: (0;1); (1;8/3) Co jest nie tak?
22 sie 17:34
henrys: Wyznacz dziedzinę funkcji
22 sie 17:36
Paula: ok, teraz rozumiem, dzięki za pomoc
22 sie 17:40
daras: nadal źle! masz w liczniku 6x(x−3) i rozwiązać nierówność> 0
22 sie 21:20
daras: rosnąca : x < o i x > 3
22 sie 21:22
daras: i nie wciskaj kitu, ze znasz jakąś ogólną zasadę
22 sie 21:22
Janek191: rysunek Df =ℛ \ {1}
 (2 x − 3)*(x2 + 3 x + 4) − (x2 − 3 x +4)*(2 x + 3) 
f '(x) =
=
 (x2 +3 x − 4)2 
 6 x2 − 16 x 
=
, x ≠ 1
 (x2 + 3 x − 4)2 
 8 
f'(x) > 0 ⇔ 6 x2 − 16 x = x*(6 x − 16) > 0 ⇔ x ∊ (−∞, 0) ∪ (
; +∞)
 3 
 8 
f '(x) < 0 ⇔ x ∊ ( 0,1) ∪ (1,
)
 3 
 8 
zatem funkcja f rośnie w przedziałach: ( − ∞ ;0 ) , (
; +∞)
 3 
 8 
oraz maleje w przedziałach: ( 0; 1) , ( 1;
).
 3 
23 sie 08:09
daras: D = ℛ \ {−4,1}
 8 
rosnąca: (−∞, −4) ∪ (−4,0) ∪ (
,∞)
 3 
 8 
malejąca: (0,1)∪(1,
)
 3 
http://www.wolframalpha.com/input/?i=%28x^2%E2%88%923x%2B4%29%2F%28x^2%2B3x%E2%88%924%29
23 sie 10:34
Janek191: Ale dałem plamę. emotka Wniosek − nie należało się spieszyć, ale spokojnie rozwiązać równanie : x2 + 3 x − 4 = 0
23 sie 13:02
daras: ja tez sie pospieszyłem i policzyłem w pamięciemotka ale to przez Paulę a właściwie jej pokrętny zapis btw ciekawe czy ją to jeszcze interesuje ?
23 sie 13:37