pochodna
bimbam: hej
| | 1 | |
czy dla x=0 jest minimum w funkcji danej wzorem y= |
| x 2+8x −2  |
| | 2 | |
Poniżej lin do rozwiązania, ale nie jestem pewien, czy autora na koniec filmy nie jest w
błędzie, mówiąc że tam nie ma minimum
https://www.youtube.com/watch?v=u_L9aZ6bPHg&index=9&list=PLWWDiQscgVtdGVOgE6i77MA29qjYReMxz
Wiem, że punktów krytycznych szukamy tam, gdzie pochodna równa się zero, albo tam gdzie
pochodna jest nieokreślona (nie istnieje).
| | 16 | |
pochodna ma wzór y`=x− |
| więc nie jest określona w punkcie x=0 |
| | x3 | |
Zatem x=0 jest punktem krytycznym, który można podejrzewać, ze jest ono ekstremum albo minimum

10 sie 19:14
Janek191:
x = 0 nie należy do dziedziny danej funkcji

10 sie 19:26
Janek191:
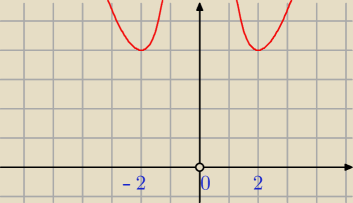
10 sie 19:38
bimbam: ale czy jest punktem krytycznym

10 sie 20:31
bimbam: czy zero jest minimum czy nie jest

10 sie 20:34
john2: nie jest, bo nie ma w tym punkcie funkcji
10 sie 21:06
bimbam: dzięki
10 sie 21:14
bimbam: a jaki byłby przypadek właśnie z tym, że pochodna jest nieokreślona, ale jednak jest ekstremum.
Czy ktoś mógłby podać jakiś przykład i wyjaśnić w kilku słowach

10 sie 21:21
john2: f(x) = |x|
10 sie 21:24
john2: f'(x) = 1 dla x > 0
f'(x) = −1 dla x < 0
pochodna zmienia znak, więc mamy minimum
10 sie 21:25
10 sie 21:30






