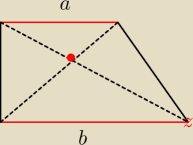
Dowód z trapezem prostokątnym z1o: Dłuższa podstawa trapezu prostokątnego ma długość a, krótsza zaś długość b. Wykaż, że odległość punktu przecięcia przekątnych trapezu od krótszego ramienia jest równa ab/(a+b).

Eta: zobacz wpis 8 czerwca 20: 28 https://matematykaszkolna.pl/forum/253102.html

pigor: ..., no cóż, moja Maja nie daje mi spokoju, a więc niech c,d − odległości punktu przecięcia się przekątnych od danych podstaw odpowiednio a,b jak na rys powyżej i x=? − szukana odległość, to 2 razy z podobieństwa ΔΔ (kkk), albo wniosku z tw.Talesa i podobieństwa : modelem mat. zadania może być np. taki układ równań: ^b_x = ^c+d_c i ^b_a = ^d_c ⇔ ^b_x = 1+^d_c i ^d_c = ^b_a ⇒ ⇒ ^b_x =1+^b_a ⇔ ^b_x = ^a+b_a ⇔ x(a+b) =ab ⇒ x= ^ab_a+b c.n.w.

x12z8: Ktoś mógłby mi wytłumaczyć skąd wziął się ten stosunek ^b_x = ^c+d_c. Nie rozumiem do którego elementu wykorzystać to tw. Talesa

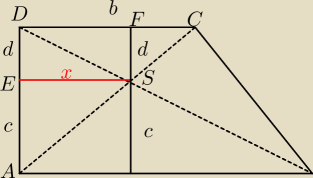
wredulus_pospolitus: z podobieństwa trójkątów ΔACD ~ ΔASE

	b		c+d
więc:		=		(patrz przyprostokątne tych dwóch trójkątów)
	x		c

x12z8: wredulus pospolitus serdeczne dzięki!