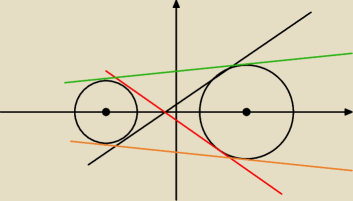
Geometria analityczna okręgi WOTTOWNIK: Siemka mam problem z takim zadankiem: Znajdź równania wspólnych stycznych do okręgów (x−10)²+y²=36 oraz (x+5)²+y²=9. narysowałem sobie rysunek ale nie wiem jak zacząć.

J: szykana styczna: y = ax + b ⇔ ax − y + b = 0 teraz wykorzystujesz wzór na odległość środka okregu od tej prostej, która jest równa promieniowi okręgu .... z otrzymanego układu równań wyliczysz a i b ( cztery styczne )

WOTTOWNIK: No mam coś takiego: |10a+b|=|2b−10a| 0=16a²+10ab+15

J: Masz układ:

I10a+bI
	= 6
√a2+1

I−5a+bI
	= 3
√a2+1

WOTTOWNIK: no tak

J: 1) I10a+bI = 6*√a²+1 /² (10a + b)² = 36(a² + 1) 2) .... analogicznie

WOTTOWNIK: no po porównaniu coś takiego otrzymałem 20a=b

J: a skąd to masz ?

WOTTOWNIK: (10a+b)²=36(a²+1) (−5a+b)²=9(a²+1) 9(10a+b)²=36(b−5a)² ... 20a=b

J: a dlaczego prawe strony mają być równe ?

J: masz uklad: (10a + b)² = 36(a²+1) (b − 5a)² = 9(a²+1)

WOTTOWNIK: no tak

WOTTOWNIK: siedzę przy tym już długo robię i nie może mi wyjść

J: masz wynik ?

J: w sensie odpowiedź ...

WOTTOWNIK: Nie tylko treść

WOTTOWNIK: Nie tylko treść

daras: tak się tego nie rozwiąże albo..btrudno należy rozwiązać 2 układy r−ń styczna ma z r−niem okręgu tylko JEDEN punkt wspólny−1 rozwiązanie Δ = 0 itd.

WOTTOWNIK: to już nic nie rozumiem

daras: to poszukaj: https://matematykaszkolna.pl/forum/201451.html

ZKS: Aż tak trudno nie jest. |10a + b| = 6√a² + 1 |b − 5a| = 3√a² + 1 ⇒ 2|b − 5a| = 6√a² + 1 |10a + b| = 2|b − 5a| 10a + b = 2b − 10a ∨ 10a + b = −2b + 10a b = 20a ∨ b = 0. Dla b = 0 5a = 3√a² + 1 25a² = 9a² + 9

	3
16a2 = 9 ⇒ a = ±
	4

dla b = 20a 15a = 9√a² + 1 225a² = 9a² + 9

	1
216a2 = 9 ⇒ a = ±
	2√6

	3		1		10
(a = ±		∧ b = 0) ∧ (a = ±		∧ b = ±		)
	4		2√6		√6

WOTTOWNIK: dzięki ZKS

ZKS: Oczywiście zgubiłem moduły tu |5a| = 3√a² + 1 oraz tutaj |15a| = 3√a² + 1.

WOTTOWNIK: a takie zadano, jestem w nim zielony Znajdź równania prostych przechodzących przez punkt P(3; 2) i odcinających na osiach układu współrzędnych odcinki OA i (OB takie, że pole trójkąta AOB jest równe 12.

daras: w takim razie niczego sie nie nauczyłeś WOTT chcesz tylko gotowców

WOTTOWNIK: daras: Ja tych zadań mam kupę. I w nich mam trudności w rozwiązaniu. W tym zadaniu w ogóle nie zrozumiałem treści. Nie wiem czy punkt O interpretować jako (0,0)

WOTTOWNIK: Może ktoś podpowiedzieć?

J: tak ... punkt: O(0,0)

	x		y
postać odcinkowa prostej:		+		= 1 a = IOAI , b = IOBI
	a		b

	1
PΔ =		a*b
	2

	3		2
z warunków zadania:		+		= 1
	a		b

WOTTOWNIK: już wolałbym zrobić 150 całek niż rypać się z tą geometrią analityczną

daras: jak rozwiążesz sam albo choć przeanalizujesz ze 20 takich zadań, to nie będziesz miał kłopotu z interpretacją i zrozum ieniem treści na tym polega samodzielna nauka

WOTTOWNIK:

⎧	ab2=12
⎩	3a+2b=1

⎧	a=3
⎩	b=8	−tak?

I teraz podstawiam punkt A i P do równania prostej y=ax+b i wyznaczam jedną prostą, a później drugą z B i P, ale nie wiem jeszcze dlaczego podstawiłem x=3 y=2 do tego wzorku

WOTTOWNIK: jakbyście mogli mi to wytłumaczyć

J:

1
	a*b = 12 ⇔ a*b = 24
2

3		2		2a
	+		= 1 ⇔ b =
a		b		a−3

	2a
a*		= 24 ⇔ 2a2 − 24a + 72 = 0 ⇒ a = 6, .... b = 4
	a−3

	x		y		2
szukana prosta:		+		= 1 ⇔ y = −		x + 4
	6		4		3

WOTTOWNIK: znowu głupi błąd

Hugo: