Styczne do dwóch okręgów Anka: Witajcie, Znajdź równania wspólnych stycznych do okręgów x²+y²−2=0 i x²+y²−4x−4=0. Doszłam do momentu:

	|b|
√2 =
	√a2+1

	|2a+b|
2√2 =
	√a2+1

I tu zupełnie doznałam zaćmienia i nie wiem co dalej... ALe wstyd.

Krzysiek: Szukam właśnie rozwiązań takiego zadania. Utknąłem w tym samym momencie

Anka: Serio, zero pomysłów? Będę bardzo wdzięczna za pomoc.

jikA:

	2|b|
{2√2 =
	√a2 + 1

	|2a + b|
{2√2 =
	√a2 + 1

2|b|		|2a + b|
	=		/ * √a2 + 1
√a2 + 1		√a2 + 1

2|b| = |2a + b| 2b = 2a + b ∨ 2b = −2a − b

	2
b = 2a ∨ b = −		a
	3

dla b = 2a otrzymujemy

	2|a|
√2 =		/ 2
	√a2 + 1

	4a2
2 =
	a2 + 1

4a² = 2a² + 2 a² = 1 ⇒ a = ±1 ∧ b = ±2

	2
dla b =		a
	3

	2   |a| 3
√2 =		/ 2
	√a2 + 1

	4   a2 9
2 =
	a2 + 1

4
	a2 = 2a2 + 2 jak widzimy to równanie ma brak rozwiązań
9

Tak więc mamy dwie proste l : y = x + 2 albo k : y = −x − 2.

Anka: Dzięki

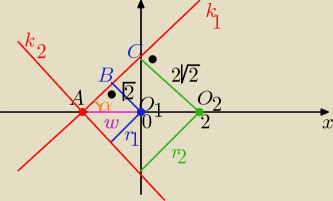
Eta: 2 sposób |O₁O₂|=2, O₁(0,0) ,O₂(2,0) , r₁=√2, r₂=2√2 z podobieństwa trójkątów ACO₂ i ABO₁

2√2		|O1O2|+w
	=		⇒ w= 2 , A(−2,0)
√2		w

	√2
to sinα=		⇒ α= 45o
	2

tgα=1 to styczna : k₁: y= 1(x+2)+0 ⇒ k₁ : y= x+2 styczna k₂ ⊥k₁ ⇒ k₂ : y= −x−2

Ania: Mam pytanko co do 1 sposobu rozwiązania czy nie powinno być b>0 v b<0 i 4 przypadki a nie dwa ? A jeśli nie to dlaczego, mógłby mi to ktoś wytłumaczyć?