Tożsamości
Marcin:
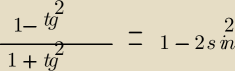
Witam proszę o pomoc w rozłożeniu licznika.
W mianowniku wyszło mi
1cos2 Lewą stronę robię.
21 lip 17:34
Bogdan:
pomnóż licznik i mianownik przez cos2x
21 lip 17:49
Marcin: po rozłożeniu tg2 ?
21 lip 17:53
daras: | | cos2 − sin2 | |
..= |
| =... |
| | cos2 + sin2 | |
stosujac twój zapis bezargumentowy

21 lip 18:32
Mila:
Nie wolno pisać funkcji trygonometrycznych bez argumentu.
21 lip 20:05
Kacper:
Cześć
Mila 
jak wakacje?

21 lip 20:06
Bogdan:
Uważam, że przy określonym założeniu można posługiwać sie taką formą zapisu
wielkości trygonometrycznych, a poza tym w tym zadaniu nie dostrzegam żadnej funkcji,
nigdzie nie występuje tu zapis w rodzaju f(x), f(α), g(t), itp.
21 lip 20:11
daras:
@
Mila w wakacje wszystko wolno

21 lip 20:14
Mila:
No cóż, za burtę wyrzuca się różne ważne wartości, to można i argumenty funkcji
trygonometrycznych.
Kacper, wakacje wspaniałe, ale trochę za gorąco. Polska to piękny kraj.
Pozdrawiam wszystkich


21 lip 21:18
21 lip 21:21
5-latek: Dobry wieczor
Milu 
Pozdrawiam również

dzisiaj już byłem w pracy drugi dzień po urlopie . Troche za goraco to mało powiedziane ,
O 17:00 33 stopnie ciepla było

21 lip 21:24
5-latek: | 1−tg2α | |
| (mnożymy licznik i mianownik przez cos2α |
| 1+tg2α | |
| 1*cos2α−tg2α*cos2α | | cos2α − sin2α | |
| = |
| = |
| 1*cos2α+tg2α*cos2α | | cos2α +sin2α | |
| | cos2α−sin2α | |
|
| (wiadomo dlaczego przez1 = cos2α−sin2α= 1−sin2α−sin2α= 1−2sin2α=P |
| | 1 | |
Skoro cos
2α+sin
2α=1 to cos
2α= 1−sin
2α lub sin
2α= 1−cos
2α
21 lip 21:46
daras: gdzie tyle było

?

ja w bluzie dzisiaj siedzę
21 lip 21:49
21 lip 21:51
5-latek: Czesc
daras 
Pozdrawiam
U mnie na Dolnym Slasku . Wiem ze nad morzem jest zimno . Rodzinka mojej koleżanki z przecy
jest wlasnie nad morzem i dzwonią do niej ze maja tam zimno .
21 lip 21:52
daras: a miałem jechać do Wrocławia

21 lip 21:57
Mila:
| | | |
= |
| = mnożę licznik i mianownik przez cos2α |
| | | |
| | cos2α−sin2α | |
= |
| = |
| | cos2+sin2α | |
=cos
2α−sin
2α=1−sin
2α−sin
2α=
=1−2sin
2α=P
==========
21 lip 22:05
Mila:
Witam
5−latku. Tak myślałam, że jesteś w pracy albo na wycieczce.

21 lip 22:06
daras: a ja nie mnożę licznika/mianownika tylko po prostu dzielę

21 lip 22:08
daras: niestety we Wrocku nie znalazłem miejscówki
21 lip 22:09
5-latek: daras na jutro zapowiadają znowu upaly .
Ale mam nadzieje ze nie będzie tak grzać bo po pracy jade do brata pomagać mu przy budowie
garażu . mamy robic szalunek na dach .
21 lip 22:13
daras: upały zapowiadają co drugi dzień
taki garaż to niezła miejscówka w przyszłym roku też będę szukał

21 lip 22:17
5-latek: 
21 lip 22:18
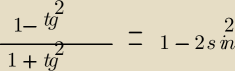 Witam proszę o pomoc w rozłożeniu licznika.
W mianowniku wyszło mi 1cos2 Lewą stronę robię.
Witam proszę o pomoc w rozłożeniu licznika.
W mianowniku wyszło mi 1cos2 Lewą stronę robię.

 jak wakacje?
jak wakacje? 



 Pozdrawiam również
Pozdrawiam również  dzisiaj już byłem w pracy drugi dzień po urlopie . Troche za goraco to mało powiedziane ,
O 17:00 33 stopnie ciepla było
dzisiaj już byłem w pracy drugi dzień po urlopie . Troche za goraco to mało powiedziane ,
O 17:00 33 stopnie ciepla było 
 ?
?  ja w bluzie dzisiaj siedzę
ja w bluzie dzisiaj siedzę
 Pozdrawiam
U mnie na Dolnym Slasku . Wiem ze nad morzem jest zimno . Rodzinka mojej koleżanki z przecy
jest wlasnie nad morzem i dzwonią do niej ze maja tam zimno .
Pozdrawiam
U mnie na Dolnym Slasku . Wiem ze nad morzem jest zimno . Rodzinka mojej koleżanki z przecy
jest wlasnie nad morzem i dzwonią do niej ze maja tam zimno .




