parametr Asmander: Dla jakiej wartości parametru m nierówność (x−3m)(x−m−3)<0 jest spełniona przez każdą liczbę rzeczywistą należącą do przedziału <1;3> Δ≥0 1≤x_w≤3 f(1)≥0 f(3)≥0 takie warunki tak?

J: Δ > 0 1 < x_w < 3 f(1) = 0 f(3) = 0

Asmander: mam takie warunki więc postanowiłem je rozwiązać, ale nie wyszło mi z odpowiedziami

	1
m∊(0,		)
	3

na początku wymnożyłem oba nawiasy (x² − (4m+3)x +3m² +9m) 1) Δ>0 Δ=4m²−12m+9 Δ=(2m−3)² > 0

	3		3
m=		m∊R−{		}
	2		2

2) f(1)=0 (1−3m)(−m−2)=0 3m²+5m−2=0

	1
m∊{−2;		}
	3

3) f(3)=0 3m² −3m=0 m(3m−3)=0 m=0 v m=1 m∊{0,1} 4)1<x_w<3

−4m−3		−4m−3
	>1 i		<3
2		2

	1		1
m∊(−2		; −1		)
	4		4

gdzie mam błąd

ZKS: Mi się wydaję, że takie powinniśmy dać warunki f(1) ≤ 0 ∧ f(3) ≤ 0 razem z Δ i x_w.

J:

	4m+3
xw =
	2

J: Racja ZKS ... , nie zwróciłem uwagi, że przedział <1,3> jest domknięty...

Asmander: 1) m∊R

	1
2) m∊<−2;		>
	3

3) m∊<0,1>

	1		3
4) m∊<−		;		>
	4		4

	1
odp. m∊<0 ;		>
	3

J: Musimy zaostrzyć warunki: f(1) < 0 oraz f(3) < 0 ( funkcja nie może w tych punktach być równa 0 , ma być ujemna)

Asmander:

	1
m∊(0,		)
	3

I teraz sie wszystko zgadza.

ZKS: Oczywiście przecież tam nie ma (1 ; 3) tylko jest [1 ; 3].

ZKS: Asmander widzę, że robisz wszystko jak automat. Pokażę Ci jak prosto te wszystkie warunki można policzyć. Na początku Δ > 0. Zauważamy, że funkcję f(x) mamy już podaną w postaci iloczynowej, lecz musimy otrzymać

	3
dwa różne pierwiastki, zatem 3m ≠ m + 3 ⇒ m ≠		.
	2

Dalej f(1) < 0 analogicznie f(3) < 0. Nic nie wymnażamy, ponieważ łatwo wszystko odczytać z postaci iloczynowej

	1
(1 − 3m)(1 − m − 3) < 0 ⇒ (3m − 1)(m + 2) < 0 ⇒ m ∊ (−2 ;		).
	3

Na końcu x_w, wykorzystujemy wiadomość, że wierzchołek jest równy średniej arytmetycznej pierwiastków funkcji kwadratowej

	x1 + x2		3m + m + 3		4m + 3
xw =		=		=
	2		2		2

	4m + 3
1 <		< 3
	2

2 < 4m + 3 < 6 −1 < 4m < 3

	1		3
−		< m <		.
	4		4

Asmander: Jakoś wole robić wszystko jak robot, bo jest mniejsza szansa na pomyłke. Wszystkie warunki przez Ciebie były wykonane bardzo sprytnie.

Asmander:

	3
3m≠m+3 ⇒ m≠
	2

i właśnie tutaj był sęk dlaczego to wszystko wymnożyłem.

Asmaner: Czemu Δ>0? a nie ≥

J: Bo dla Δ = 0 funkcja przyjmowałaby tylko wartości nieujemne

Asmaner: Przeciez Δ informuje tylko o ilości miejsc zerowych , 2, ,1, lub wcale

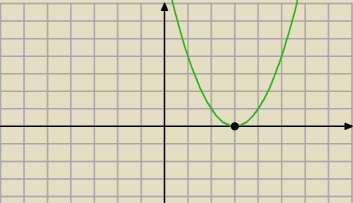
J: A teraz widzisz ?

Asmaner: Nie wytłumacz

J: dla: a > 0 i Δ = 0 ( jak na rysunku ) funkcja nie przyjmuje wartości ujemnych

Asmaner: Zatem zeby ta funkcja osiagała wartości ujemne Δ<0 i a<0 wiec skąd Δ>0

Asmander: (x−3m)(x−m−3)<0 bo a>0 i Δ>0 wtedy i tylko wtedy przyjmuje wartości ujemne

Asmander: https://matematykaszkolna.pl/strona/79.html przypatrz się temu

J: przestań bredzić .... jak a > 0 i Δ > 0 , wtedy funkcja ma dwa miejsca zerowe i przyjmuje zrówno wartości dodatnie, ujemne i równe zero ( trzeci rysunek u góry )

Asmaner: DOBRA CZAJE

Kacper: Mozna było skorzystać z postaci iloczynowej