Oblicz współrzędne punktu C Shadowplay: Punkty A(−3,1) i B(2,−1) są wierzchołkami trójkąta ABC. Odcinek AC jest zawarty w prostej y=2x+7, a jedna ze środkowych trójkąta ma równanie y=x+4. Oblicz współrzędne punktu C. Środkowa y=x+4 to środkowa boku |BC| ponieważ 2=−1+4 Zadanie rozwiązuję ze wzorów na współczynnik kierunkowy prostej C (x,y)

	x+3
Współczynnik AC a1=2, więc 2 =
	y−1

	x−2
Współczynnik BC a2=−1, więc −1 =
	y+1

Rozwiązując tak zadanie wychodzi zły wynik. Znalazłam już inny sposób na rozwiązanie tego zadania jednak chciałabym wiedzieć co jest źle w sposobie pokazanym powyżej..

5-latek: 2=−1+4 (ale to nie jest prawda

Shadowplay: Już poprawiam: −3+4=1

Shadowplay: Inaczej. Jest to środkowa BC ponieważ:

	2
−środkowa AB miałaby współczynnik
	5

	1
−a środkowa AC −
	2

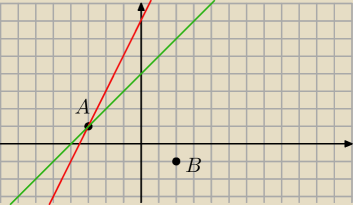
5-latek: y=2x+7 (czerwona y=x+4 (zielona Już z rysunku widać ze to będzie srodkowa boku BC

Shadowplay: Czyli współczynnik prostej do której należy BC będzie równy −1, tak jak podstawiłam w zadaniu

Shadowplay: Dalej nie wiem, gdzie w moim rozumowaniu jest błąd Proszę o pomoc

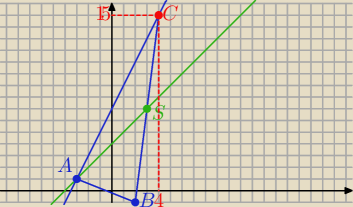
Eta: A(−3,1)∊ do y=x+4 bo 1=−3+4 ⇒ 1=1 środkowa AS ma równanie y=x+4 i C∊ AC ⇒C(x, 2x+7)

	xC+xB		yC+yB
S środek odcinka BC to : xS=		i yS=
	2		2

	x+2		2x+7−1
xS=		i yS=		= x+3 i S∊y=x+4
	2		2

	x+2
zatem: x+3=		+4 ⇒ 2x+6=x+2+8 ⇒ x=4 to y=2*4+7= 15
	2

odp: C(4,15) i S(x, x+3)=(3,7)

Mila: Witaj Eto, forumowicz prosi Cię o wyjaśnienie Twojego sposobu. https://matematykaszkolna.pl/forum/46979.html

Shadowplay: Dziękuję, ale mi chodziło o wytknięcie błędu w moim sposobie rozwiązania tego zdania