Prostokąt, którego przekątne zostały podzielone na 3 równe części Shadowplay: Z przeciwległych wierzchołków prostokąta poprowadzono dwa odcinki prostopadłe do jego przekątnej i dzielące ją na trzy równe części. Wiedząc, że dłuższy bok ma długość 5cm., oblicz długość krótszego boku i pole tego prostokąta.

x&y: Szukajcie, a znajdziecie https://matematykaszkolna.pl/forum/296072.html

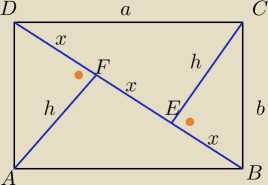
Shadowplay: A czy rozwiązywanie tego układem równań: a, b − długości boków trójkąta, a=5cm h − wysokość x − dł przekątnej podzielonej na 3 części ab = 1/2 * 2* 2xh+ 1/2 * 2xh → ab=3xh a² + b² = 9x² h² + x² = b² Nie znamy h, x ,b Czy tak może być? Jeśli nie, to co jest źle?

Kacper: Rozwiązać − ocenić poprawność − wyciągnąć wnioski.

Shadowplay: Rozwiązanie nie jest poprawne, ale nie potrafię wywnioskować dlaczego

Mila: Twoje obliczenia : a² + b² = 9x² h² + x² = b² cd. h=√2x*x Wysokość opuszczona z wierzchołka kąta prostego jest równa średniej geometrycznej długości odcinków, na które podzieliła przeciwprostokątną. ( to wynika z podobieństwa odpowiednich trójkątów) h²=2x² 2x²+x²=b² 3x²=b² a²+b²=9x² 25+3x²=9x² 25=6x² Dalej licz sam