#EGZAMIN#2# bezendu:

	x
Obliczyć pochodną kierunkową funkcji f(x,y)=		w punkcie (x0, y0
	√x2−2y2

	3π
) = (2,1) w kierunku wersora 𝑣⃗ tworzącego kąt α=		z dodatnią częścią osi ox
	4

Moje rozwiązanie w linku. http://zapodaj.net/6eaac27466a41.jpg.html

bezendu: .

bezendu: ?

bezendu: ?

bezendu: ?

bezendu: Up

bezendu:

	y
Całka ∬D		dxdy 1≤x2+y2≤9 x≥y≥0
	x4

Może ktoś podać wynik, bo chcę sprawdzić poprawność.

Mila: Pochodne cząstkowe dobrze , wartości prawidłowo obliczone, jeśli chodzi o dalsze, to nie pamiętam wzorów. Możesz pochodne cząstkowe napisać w takiej postaci, lepiej (chyba) liczyć wartości.

df		−2y2
	=
dx		√(x2−2y2)3

df		2xy
	=
dy		√(x2−2y2)3

bezendu: Z tą całką wychodzi mi cały czas wynik ujemny.

Mila: Z 21:20 ?

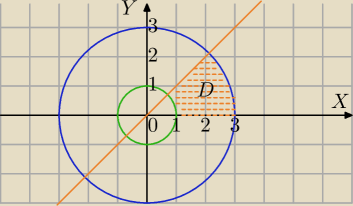
Mila: Taki masz ustalony obszar?

bezendu: Tak. obszar całkowania wychodzi mi 1≤r≤3 π/4≤φ≤π/2 po podstawieniu mam całkę Nie pisałem już granic całkwoania tutaj

	y		r2sinφ
∬D		dxdy=∫{∫		dφ}dr
	x4		r4cos4φ

	r2sinφ		1		sinφ
∫		dφ=		∫		dφ
	r4cos4φ		r2		cos4φ

t=cosφ dt=−sinφdφ

	−1		1
=		∫t−4dt=		+C
	r2		3r2cos3φ

Czy do tej pory jest ok ?

bezendu: a i obszar całkowania mam nad prostą y=x

Mila: Wydaje mi się, że :

	π
0≤φ≤
	4

Mila: y≤x to pod prostą i nad osią OX.

bezendu: Racja, a całka ?

Mila:

2
	*(2√2−1)
9

bezendu: Ale czy to co przedstawiłem do tej pory jest ok ?

Mila: Wydaje mi się,że tak, poszukam jeszcze w notatkach. Jutro, bo teraz nie mam dostępu do szafki. Może ICSP tu spojrzy.

bezendu:

	2
Widziałem gdzieś podobną całkę. Wynik teraz mi wyszedł		(−4+8√2) ?
	9

Mila:

	1		1
1∫3(		([		]0π4)dr=
	3r2		cos3φ

	1		1		1
=1∫3(		*(		−		) dr=
	3r2		π   cos3   4		cos0

	1		2
=1∫3[		*((		)3−1)]dr=
	3r2		√2

	1
=1∫3[		*(2√2−1)] dr=
	3r2

	2√2−1		1
=		1∫3(		)dr=
	3		r2

= licz teraz do końca

bezendu:

	2
Ok, wyszło teraz		(−1+2√2) dziękuję bardzo !
	9

Mila:

Mila: Tu masz podobną całkę: https://matematykaszkolna.pl/forum/296441.html

bezendu: Widziałem, ale tamta się różni obszarem i jest jeszcze źle zrobiona i jest na odwrót

Mila: Obszar inny, możesz rozwiązać, dla treningu.

bezendu: Dobrze zrobię po 01:00 teraz trochę pospać, egzamin dopiero we wtorek Jeszcze w poniedziałek mam jeden też muszę się pouczyć.

Mila: W ogóle to idź spać. Dobranoc.