obszar 2
Miłosz:
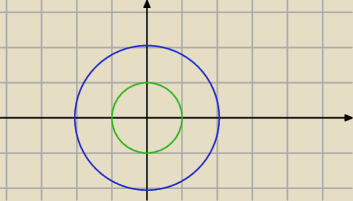
Jak zaznaczyć taki obszar 1≤x
2+y
2≤4 i y≥x≥0
?
26 cze 16:45
Miłosz: ?
26 cze 17:27
Benny: No masz ten pierścień, ale bierzesz tylko 1 ćwiartkę, bo x i y ≥0
26 cze 17:30
Saizou : pierwszą ćwiartkę i dodatnie półosie

26 cze 17:34
Miłosz:
Ok, to teraz będzie poważniejszy problem, bo muszę całkę
| | x | |
podwójną |
| dxdy policzyć po tym obszarze  |
| | y2 | |
26 cze 17:36
ICSP: No to w czym problem ?
Opisać twój obszar za pomocą współrzędnych biegunowych.
26 cze 17:40
ICSP: oczywiście nie będzie to cała pierwsza ćwiartka jak koledzy sugerują, zacznij od poprawnego
rysunku.
26 cze 17:41
Miłosz:
| | x | |
sorry tam jest całka ∫∫D |
| dxdy |
| | y4 | |
x=rcosφ
y=rsinφ
1≤r≤2 ?
≤φ≤
potem nie wiem jak wyznaczyć ten kąt
26 cze 17:44
Miłosz:
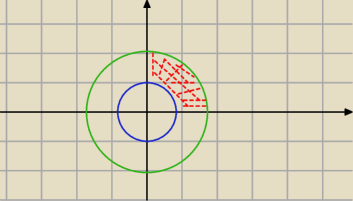
26 cze 17:45
ICSP: zły rysunek zbioru. Jeszcze raz.
26 cze 17:46
Miłosz:
Krawędzie też należą

I chyba teraz ok
26 cze 17:51
ICSP: Nie będzie dobrze, ale zadam pytanie pomocnicze :
Jaki zbiór opisuje nierówność y ≥ x ?
26 cze 17:52
Miłosz:
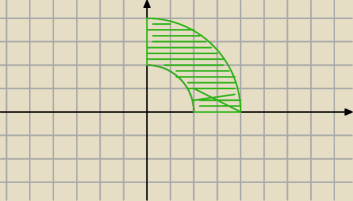
26 cze 17:53
ICSP: Nadal źle

26 cze 17:55
Miłosz:
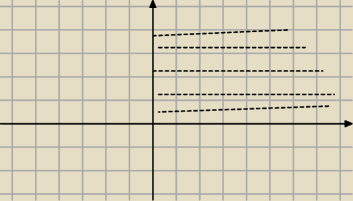
26 cze 17:58
ICSP: Nie, coś prostszego :
y = x
26 cze 18:01
Miłosz:
Dobrze ale co mi to da dla mojego obszaru ?
26 cze 18:06
ICSP: Jeżeli narysujesz y = x to narysujesz y ≥ x i narysujesz y ≥ x ≥ 0
26 cze 18:09
ICSP: Potem "nałożenie" na to pierścienia nie powinno być już problemem.
26 cze 18:09
Miłosz:
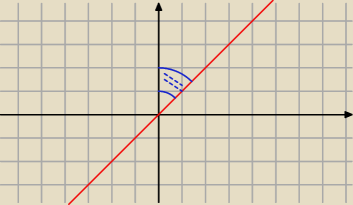
ok ?
26 cze 18:13
ICSP: Mamy to.
Teraz warunki na r oraz α
x = rcosα , y = rsinα
z podwójnej nierówności : 1 ≤ x
2 + y
2 ≤ 4 wyliczamy r :
1 ≤ r
2(sin
2α + cos
2α) ≤ 4
1 ≤ r ≤ 2
Z podwójnej nierówności : y ≥ x ≥ 0 wyliczamy α :
| | π | |
sinα ≥ cosα ≥ 0 oraz α < |
| |
| | 2 | |
Dzieląc stronami przez cosα ≥ 0
| | π | | π | |
tgα ≥ 1 ⇒ α ≥ |
| i α ≤ |
| |
| | 4 | | 2 | |
Dalej już prosto:
| | x | | r2cosα | |
∫∫ |
| dxdy = ∫∫ |
| drdα pod odpowiednich granicach oczywiście. |
| | y4 | | r4sin4α | |
26 cze 18:15
ICSP: cosα > 0 , nie chcemy przecież dzielić przez 0
26 cze 18:16
Miłosz:
Dziękuję.
26 cze 18:22
27 cze 21:02
Mila:
Dobrze.
Popraw zapisy, w jednym zapisie granice φ, nie opuszczaj dr.
Obliczenia w porządku.
28 cze 21:45
 Jak zaznaczyć taki obszar 1≤x2+y2≤4 i y≥x≥0
?
Jak zaznaczyć taki obszar 1≤x2+y2≤4 i y≥x≥0
?



 I chyba teraz ok
I chyba teraz ok



 ok ?
ok ?