Maraton
anaisy: Nie znalazłam aktualnego tematu tego typu i myślę, że fajnie byłoby go założyć. Proponuję taką
zabawę: jedna osoba wrzuca jakieś zadanko, najlepiej nie wymagające hardej teorii (mam tu na
myśli rzeczy z któregoś roku studiów, o których słyszała mała liczba maturzystów), tylko
takie, które można rozwiązać jakoś sprytnie. Pozostali próbują rozwiązać, jeśli komuś się uda,
proponuje następny problem. I tak w nieskończoność

(chyba, że znajdzie się coś wyjątkowo
trudnego, wtedy fajnie będzie jeśli autor po pewnym czasie poda swoje rozwiązanie lub
wskazówki).
To na początek coś takiego:
Problem 1.:
Niech D będzie spodkiem wysokości poprowadzonej z wierzchołka A w trójkącie ABC. Rozważmy
punkty E i F leżące odpowiednio na odcinkach AB i AC takie że proste AB i DE oraz proste CA i
DF są prostopadłe. Udowodnij, że punkty B, C, F, E leżą na jednym okręgu.
21 cze 20:03
b.: To chyba bardziej sztafeta niż maraton, ale pomysł fajny

22 cze 08:57
AS: Po raz trzeci podaję propozycję zadania,ale nikt nie kwapił
się do jego rozwiązania.Oto zadanie:
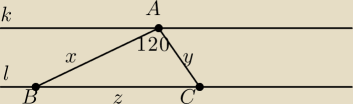
Dane są dwie równoległe proste w odległości h jedna od drugiej
i dowolny punkt A.
Przez A poprowadzić dwie proste pod kątem 120o tak,żeby jedna
z nich przecięła proste równoległe w punktach B i B1,druga zaś przecięła
je odpowiednio w punktach C i C1, przy czym ma być spełniony warunek
BB1 + CC1 = m.
Zastosować: h = 1 , m = 5.
22 cze 09:36
===:
Kolego
AS ... zadań nie piszemy ze słyszenia jeno dokładnie przepisujemy treść
... bo inaczej wychodzi z tego zagadka.
Sam chociaż wiesz co należy policzyć


22 cze 14:30
anaisy:
Dlaczego tak bardzo na liczenie

?
No ale dobra. Załóżmy sobie że te proste to k i l, punkty B, C leżą na prostej l a punkty B' C'
na prostej k. Na początku rozważymy przypadek w którym A leży na k (wtedy a pokrywa się z B' i
z C'). Zastanówmy się jakie będą długości odcinków AB i AC (b.s.o AB>AC), gdy ∡BAC=120[deg].
Niech AB=x, AC=y i BC=z. Wystarczy, że rozwiążemy układ równań:
x+y=5
| z | | 1 | |
| = |
| xycos(120[deg]) (ze wzorów na pole trójkąta w ABC) |
| 2 | | 2 | |
x
2+y
2−2xycos(120[deg]))=z
2 (z tw. cosinusów)
No to po uproszczeniu:
x+y=5
x
2+y
2+xy=z
2
czyli
x+y=5
(x+y)
2−xy=z
2
Z tych trzech równań otrzymujemy więc
| | xy√3 | | 3x2y2 | |
52−xy=( |
| )2 ⇒ 25−xy= |
| , |
| | 2 | | 4 | |
| | 4√19−2 | |
Patrzymy na to jak na równanie kwadratowe względem xy i mamy xy= |
| . |
| | 3 | |
| | 2√19−1 | |
Podstawiamy do drugiego równania i mamy z= |
| , a następnie do trzeciego |
| | √3 | |
| | 2√19−1 | | 77−4√19 | |
(x+y)2−xy=( |
| )2= |
| , skąd |
| | √3 | | 3 | |
| | 77−4√19 | | 4√19−2 | | 77−4√19−12√19+6 | | 83−16√19 | |
(x+y)2−4xy= |
| −3* |
| = |
| = |
| . |
| | 3 | | 3 | | 3 | | 3 | |
| | 83−16√19 | | 8−√19 | |
Założyliśmy, że x≥y, więc mamy (x−y)2= |
| , skąd x−y= |
| , co w |
| | 3 | | √3 | |
połączeniu z równaniem x+y=5 daje nam
Odcinek długości
√3 konstruujemy rysując trójkąt prostokątny o przyprostokątnej 1 i
przeciwprostokątnej 2, a odcinek
√57 rysując trójkąt prostokątny o przeciwprostokątnej 29 i
przyprostokątnej 28. Jesteśmy zatem w stanie skonstruować odcinki 15+8
√3−
√57 i
15−8
√3+
√57. Wystarczy zatem udowodnić, że dla odcinka o długości a jesteśmy w stanie
skonstruować odcinek 6 razy krótszy, a to już jest bardzo proste− rysujemy trójkąt prostokątny
o przyprostokątnych a i 6a. Teraz na dłuższej przyprostokątnej zaznaczamy punkt w odległości
5a od wierzchołka przy kącie 90[deg] w tym trójkącie. Rysujemy prostą prostopadłą do odcinka
6a przechodzącą przez ten punkt i mamy szukany odcinek.
No to gdy już wiemy, co się dzieje, gdy A leży na prostej k, to teraz zaznaczmy sobie dowolny
punkt A'. Wystarczy, że narysujemy proste równoległe do AB i AC i mamy
KONIEC.
Ale następnym razem AS najpierw rozwiązujemy poprzednie zadanie, a dopiero później wrzucamy
swoje.
Oczywiście to jest aktualne zadanko:
Problem 1.:
Niech D będzie spodkiem wysokości poprowadzonej z wierzchołka A w trójkącie ABC. Rozważmy
punkty E i F leżące odpowiednio na odcinkach AB i AC takie że proste AB i DE oraz proste CA i
DF są prostopadłe. Udowodnij, że punkty B, C, F, E leżą na jednym okręgu.
22 cze 15:05
AS:
1. Nie rozumiem treści zarzutu ani kto je postawił.
2. Nigdzie nie znalazłem regulaminu który by tę sprawę regulował.
3. Jeżeli już problem znalazł się na Forum to proponuję swoje
rozwiązanie
4. Amen
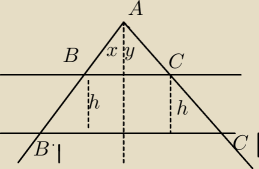
1 x + y = 120
o
2. BB1 = h/cos(x) , CC1 = h/cos(y)
Z warunku postawionym w zadaniu zachodzi
h/cos(x) + h/cos(y) = m
Do rozwiązania równanie
h*cos(y) + h*cos(x) = m*cos(x)*cos(y)
Po podstawieniu h i m mamy
cos(y) + cos(x) = 5*cosx*cos(y)
22 cze 15:58
anaisy: AS, rozumiem, że przedstawiasz inne niż moje rozwiązanie swojego zadania. Ciekawi mnie w jaki
sposób rozwiązujesz to równanie: cos(y) + cos(x) = 5*cosx*cos(y).
22 cze 16:43
AS: podaję skrótowo
Z pierwszego równania mamy y = 120 − x
Wstawiając do ostatnio podanego równania mamy
cos(120 − x) + cos(x) = 5*cos(x)*cos(120 − x)
cos(120 − x) = cos(90 + 30 − x) = −sin(30 − x)
czyli
cos(x) − sin(30 − x) = −5*cos(x)*sin(30 − x)
Po rozwinięciu i uporządkowaniu otrzymałem
5*cos
2(x) − 5*
√3*sin(x)*cos(x) − 3*cos(x) − 5*sin(x) = 0
| | 1 − t2 | | 2*t | |
Podstawiając cos(x) = |
| , sin(x) = |
| |
| | 1 + t2 | | 1 + t2 | |
gdzie t = tg(x/2) otrzymuje po uporządkowaniu równanie stopnia 4−go
9*t
4 − 10*t
3 + 10*(
√3 − 1)*t
2 − 10*(
√3 + 1)*t + 5 = 0
Wolfram podał jako rozwiązanie tego równania x = 25.1417
22 cze 17:49
AS: Dopisek
Oczywiście podane rozwiązanie dotyczy równania
w postaci trygonometrycznej.
22 cze 17:53
anaisy: No to teraz myślimy nad problemem 1.

.
22 cze 18:01
===:
... i czegóż Ty AS nie rozumiesz. Nie napisałeś pełnej treści zadania ot i tyle.
22 cze 18:04
anaisy: Jak to, ===? Przecież w zadaniu jest polecenie poprowadzić (czyli synonim skonstruować) dane
proste.
22 cze 18:08
===:
... Ty
anaisy odczytujesz, że skonstruować a
AS liczy kąty ...
więc gdzie ta jednoznaczność

?
22 cze 18:31
anaisy: Nie mam pojęcia, jaki jest związek z liczeniem kątów przez AS i z treścią zadania, natomiast
sformułowanie wydaje mi się jednoznaczne.
Ale nie zastanawiajmy się już nad tym, myślę, że już nikt nie chce nic dodać do rozwiązania
problemu AS. Przejdźmy wreszcie do rozwiązania problemu 1. bo robi się mały off−top.
22 cze 18:40
Eta:
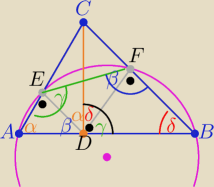
Jeżeli punkty A,B,E,F leżą na okręgu , to czworokąt ABEF jest wpisany w okrąg,
to z warunku wpisania czworokąta w okrąg mamy:
β+90
o+α=180
o ⇒ α+β= 90
o i γ+90
o+δ=180
o ⇒ γ+δ= 90
o
Taka zależność między kątami zachodzi
bo DC jest wysokością opuszczoną na bok AB
to |∡ADC|= 90
o= α+β i |∡BDC|= γ+δ= 90
o
zatem punkty A,B, E, F , leżą na jednym okręgu
c.n.u
22 cze 22:55
AS: Problem 2
Wykazać,że
| | a − b | | b − c | | c − a | | c | | a | | b | |
( |
| + |
| + |
| )*( |
| + |
| + |
| )= 9 |
| | c | | a | | b | | a − b | | b − c | | c − a | |
jeżeli a + b + c = 0
23 cze 09:15
Jola:
Eto, a skąd wiadomo, że β przy wierzchołku D jest to samo co β przy wierzchołku F
i analogicznie z kątem γ?
23 cze 12:37
anaisy: Najprościej to chyba wynika z faktu, że okrąg opisany na czworokącie CFDE jest styczny do
prostej AB (bo ∡CFD=∡CDA). Chyba, że chodziło o coś innego, Eta?
Rozwiązanie problemu 2., najbardziej pałowniczo, jak tylko się dało (przy założeniu, że a,b,c
są parami różne i różne od 0

):
No to wyrażenie
sprowadzamy sobie do wspólnego mianownika i mamy
| a−b | | b−c | | c−a | | a2b−ab2+b2c−bc2+c2a−ca2 | |
| + |
| + |
| = |
| = |
| c | | a | | b | | abc | |
| (−abc+a2b)−(ab2+b2c)−*ca2+c2a)−(bc2+abc) | |
| = |
| abc | |
| ab(−c+a)−b2(−c+a)−ac(a−c)+bc(−c+a) | | (a−c)(ab−b2−ac+bc) | |
| = |
| = |
| abc | | abc | |
| (a−c)(b(a−b)−c(a−b)) | | (a−b)(b−c)(c−a) | |
| =− |
| . |
| abc | | abc | |
Stąd
| | a−b | | b−c | | c−a | | c | | a | | b | |
( |
| + |
| + |
| )( |
| + |
| + |
| )= |
| | c | | a | | b | | a−b | | b−c | | c−a | |
| | a−b | | b−c | | c−a | | c(b−c)(c−a)+a(a−b)(c−a)+b(b−c)(a−b) | |
=( |
| + |
| + |
| )* |
| = |
| | c | | a | | b | | (a−b)(b−c)(c−a) | |
| | c(b−c)(c−a)+a(a−b)(c−a)+b(b−c)(a−b) | | (c−a)(cb−c2+a2−ab)+b(b−c)(a−b) | |
=− |
| =− |
| = |
| | abc | | abc | |
| | −(c−a)2(a+c−b)+b(b−c)(a−b) | |
=− |
| =A |
| | abc | |
Teraz z założenia mamy a+c−b=−2b, zatem
| | 2b(c−a)2+b(b−c)(a−b) | | 2(c−a)2+(b−c)(a−b) | |
A=− |
| =− |
| = |
| | abc | | ac | |
| | 2c2−4ac+2a2+ab−b2−ac+bc | | 2c2+2a2+ab+bc−b2 | |
− |
| =−( |
| −5)= |
| | ac | | ac | |
| | 2c2+2a2−(a+c)2−(a+c)2 | | 4ac | |
−( |
| −5)=−( |
| −5)=9 |
| | ac | | ac | |
Problem 3. Dana jest liczba całkowita dodatnia n, której suma wszystkich dodatnich
dzielników jest równa 2n. Udowodnij, że suma odwrotności wszystkich dodatnich dzielników
liczby n jest całkowita.
24 cze 14:52
AS: mała korekta do końcówki rozwiązania problemu 2
| | −4ac | |
... = −( |
| − 5) = 9 |
| | ac | |
24 cze 18:11
AS: Podaje moje rozwiązanie problemu 2
Pierwszy iloczyn
| | a −b | | b − c | | c − a | | c | |
( |
| + |
| + |
| )* |
| = |
| | c | | a | | b | | a − b | |
| | c | | b − c | | c − a | |
1 + |
| *( |
| + |
| ) = |
| | a − b | | a | | b | |
| | c | | b2 − b*c + a*c − a2 | |
=1 + |
| *( |
| ) = |
| | a − b | | a*b | |
| | c | | (b + a)*(b − a) − c*(b −a) | |
= 1 + |
| *[ |
| ] = |
| | a − b | | ab | |
| | c | | −c*(b − a) − c*(b − a) | | 2*c2 | |
=1 + |
| *[ |
| ] = 1 + |
| |
| | a − b | | a*b | | a*b | |
Podobnie postępując z następnymi iloczynami mamy
| | 2*a2 | | 2*b2 | |
1 + |
| i 1 + |
| |
| | b*c | | c*a | |
| | 2*c2 | | 2*a2 | | 2*b2 | |
S = 1 + |
| + 1 + |
| + 1 + |
| = |
| | a*b | | b*c | | c*a | |
| | a3 + b3 + c3 | | 3*a*b*c | |
3 + 2* |
| = 3 + 2* |
| = 9 |
| | a*b*c | | a*b*c | |
a
3 + b
3 + c
3 = (−c − b)
3 + b
3 + c
3 =
−c
3 − b
3 − 3*b*c*(b + c) + b
3 + c
3 = 3*a*b*c
24 cze 18:47
henrys:
Niech D={1,a
1,a
2,...,a
k,b
1,b
2,..b
k,n} będzie zbiorem dzielników liczby n.
a
1b
1=a
2b
2=...a
kb
k=n
1+a
1+a
2+..+b
k+n=2n
| | 1 | | 1 | | 1 | | 1 | | n | | b1 | | b2 | | ak | | 1 | |
1+ |
| + |
| +... |
| + |
| = |
| + |
| + |
| +...+ |
| + |
| = |
| | a1 | | a2 | | bk | | n | | n | | n | | n | | n | | n | |
| | n+b1+...bk+a1+..+ak+1 | |
= |
| =2 |
| | n | |
Chyba jakoś tak to ma wyglądać

25 cze 18:31
anaisy: Generalnie o to chodzi, tylko mała uwaga. Może się zdarzyć, że liczba dzielników n jest
nieparzysta, wtedy nie można tak sparować liczb a
1, ..., a
k z liczbami b
1, ... b
k. Wtedy
po prostu oznaczamy wszystkie dzielniki przez d
1, d
2, ..., d
s i mówimy że dzielnik d
m
parujemy z dzielnikiem d
s+1−m.
Czekamy na Twój problem
henrys 
.
25 cze 19:54
henrys: Tak się pewnie zdarzy jeżeli liczba n będzie kwadratem liczby naturalnej i tego nie zapisałem.
Wtedy paruję go z tym samym i na jedno wychodzi. czy coś źle widzę?
Myślę nad zadaniem

25 cze 20:00
henrys: Problem 4
Dany jest pięciokąt wypukły, którego każdy wierzchołek ma obie współrzędne
całkowite. Udowodnij, że wewnątrz tego pięciokąta znajduje się co najmniej
jeden punkt, którego współrzędne są liczbami całkowitymi.
25 cze 20:32
anaisy: Masz rację, ale to jest to samo, co napisałam wcześniej

.
Rozwiązanie problemu 4.:
Rozumiem, że ten punkt może znajdować się też na boku tego pięciokąta? (inaczej nie działa dla
pięciokąta (0,0), (2,0), (2,1), (1, 2), (0,1).
Załóżmy, że mamy pięciokąt A
1A
2A
3A
4A
5, przy czym jego wierzchołki mają odpowiednio
współrzędne A
k=(x
k, y
k) dla k∊[1,5]
Załóżmy, że wewnątrz pięciokąta nie istnieje żaden punkt. To oznacza, że |x
n−x
m|<2 (1) oraz
|y
n−y
m|<2 (2)dla dowolnych n,m∊[1,5]. Z zasady szufladkowej Dirichleta mamy, że istnieje
taki zbiór trzech wierzchołków (niekoniecznie kolejnych) danego pięciokąta
{X
1, X
2, X
3}⊂{A
1, A
2, ... , A
5}
że X
1=(a
1, b
1), X
2=(a
2, b
2), X
3=(a
3, b
3) oraz a
1≡a
2≡a
3 (mod 2), zatem z nierówności
(1) wynika, że a
1=a
2=a
3. Ponadto z zasady szufladkowej Dirichleta wynika, że dwie spośród
liczb b
1, b
2, b
3 mają tę samą parzystość, załóżmy baz straty ogólności, że b
1 i b
2.
Analogicznie mamy b
1=b
2 lub |b
1−b
2|≥2, zatem z (2) mamy b
1 =b
2. Stąd wniosek, że punkty
X
1 i X
2 się pokrywają, zatem sprzeczność, zatem conajmniej jedna z nierówności (1), (2) jest
nieprawdziwa, co kończy dowód.
___________
Zaraz znajdę następne zadanko.
25 cze 21:07
henrys: Czekaj czekaj

Nie na boku tylko wewnątrz

25 cze 21:12
henrys: Wewnątrz pięciokata który podałaś też jest taki punkt (1,1)
25 cze 21:15
AS: Podaję do rozwiązania zadanie łatwe,ale nie typowe,
nie podawane na FORUM. Oto one
Problem 5
Wykreślić konstrukcyjnie (cyrkiel,linijka,ołówek) trójkąt
mając dane obwód trójkąta m (odcinek) i dwa kąty
wewnętrzne α i β.
27 cze 10:24
henrys: Problem 4 jest rzeczywiście bardzo bardzo trudny. Chciałem się nim podzielić gdyż uważam, że
sama analiza wiele uczy. Znam dwa rozwiązania, które niestety nie są moje. Zachęcam i sam
nadal nad nim myślę.

27 cze 10:49
anaisy: Ok, powinno być.
Rozwiązanie problemu 4.:
Oznaczmy dany pięciokąt P
0 i załóżmy, że wewnątrz niego nie leży żaden punkt kratowy.
Z mojego poprzedniego dowodu mamy, że istnieje odcinek A
kA
k+1 (przyjmujemy, że
A
m=A
m (mod 5) +1), na którym istnieje punkt S mający obie współrzędne całkowite. Rozważmy
teraz taką operację: łączymy punkty A
k−1 i S, otrzymując wielokąt
A
1A
2...A
k−1SA
k+1...A
5. Następnie powtarzajmy tę operację (biorąc jakiś bok na którym
leży punkt kratowy) i niech P
r będzie wielokątem po r−tej operacji. Możemy zauważyć, że
1) jeśli wielokąt P
r nie miał wewnątrz punktu kratowego to wielokąt P
r+1 też nie ma
2) P
r>P
r+1
3) P
r zawsze jest wypukły
4) z wcześniejszego dowodu na którymś z boków będzie istniał punkt kratowy, zatem operację
możemy powtarzać w nieskończoność
Niech B
r oznacza liczbę punktów leżących na bokach P
r (łącznie z wierzchołkami). Wtedy ze
| | Br | |
wzoru Picka mamy [Pr]= |
| −1. Z (2) wynika, że Br>Br+1, stąd ponieważ Bk są zawsze |
| | 2 | |
całkowite, więc istnieje x, że B
x<5, sprzeczność.
27 cze 17:06
anaisy:
Rozwiązanie problemu 5.:
Najpierw konstruujemy dowolny trójkąt ABC, o kątach ∡A=α i ∡B=β, który ma obwód różny od m
(jest to bardzo proste, wystarczy przyjąć AB=m). Teraz na prostej AB zaznaczmy takie punkty A'
i B', że A'A=AC i B'B=BC, punkty A, B leżą na odcinku A'B' oraz A leży bliżej A' niż B.
Rozważmy dowolny prostokąt ABKL. Ponieważ A'B'≠LK, więc proste A'L i B'K przecinają się w
pewnym punkcie S. Niech prosta LK przecina proste AS i BS odpowiednio w M i N. Z tw. Talesa
mamy, że trójkąty SKL i SB'A' są podobne, zatem trójkąt o bokach LM, MN, NK jest podobny do
trójkąta ABC i ma obwód m.
27 cze 17:15
anaisy: Problem 6
Dana jest funkcja f:R→R spełniająca równość x+f(x)=f(f(x)) dla każdego x∊R. Znajdź wszystkie
liczby rzeczywiste a, dla których f(f(a))=0.
27 cze 17:27
henrys: 4) Liczba punktów kratowych na brzegu jest skończona więc tutaj już chyba mogłabyś zakończyć
dowód. W r tym kroku zostaje odcinek, który zawiera punkt kratowy leżący na przekątnej, a z
wypukłości pięciokąta należy do jego wnętrza, ale ze wzorem Picka też ładnie

27 cze 18:13
AS:
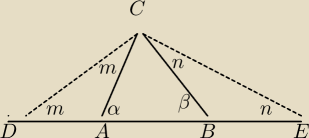
Proponuję takie rozwiązanie problemu 4.
Zacznę od analizy
Niech ΔABC będzie szukanym trójkątem.
Odkładając odcinek DA = AC i EB = BC na prostej DE
mamy odcinek DE = m , trójkąty DAC i EBC są równoramienne
a kąty odpowiednio równe kąt m = α/2 i kąt n = β/2
Już staje się jasne jak poprowadzić konstrukcję.
Rozwiązanie
1. Na prostej odłożyć odcinek DE = m
2.Przy punkcie D odłożyć kąt ADC = α/2 a przy punkcie E kąt β/2
3.Ramiona tych kątów w przecięciu wyznaczą punkt C
4.Przy punkcie C odkładamy kąt DCA = α/2 i kąt ECB = β/2
5. Ramiona tych kątów wyznaczą szukane punkty A i B.
6. W ten sposób uzyskaliśmy szukany trójkąt ABC
27 cze 19:43
Marcell:
problem 7
Wykreśl konstrukcyjnie trzy okręgi wzajemnie styczne zewnętrznie o różnych długościach
promieni znając położenie ich środków.
Podaj opis konstrukcji.
28 cze 13:31
krzyś:
problem 8
wykreśl konstrukcyjnie odcinek długości 4√2
28 cze 14:09
anaisy: ej, ale najpierw rozwiązujemy poprzednie zadanka, a dopiero później wrzucamy swoje

. Aktualny
jest problem 6.
28 cze 14:34
Mariusz: krzyś dwa razy konstrukcja średniej geometrycznej powinna załatwić sprawę
Można też konstrukcję średniej geometrycznej połączyć z twierdzeniem Pitagorasa
28 cze 17:10
krzyś:
@
Mariusz
he he ... ja to wiem

Zadanie jest po to, by Inni ( jak tu zajrzą) też to wiedzieli.
28 cze 20:46
Mariusz: Skoro ja to wiem to ten problem dość jest dość łatwy
Masz pomysł na problem 6.
28 cze 21:49
anaisy: Ok, to podpowiedź do P6.:
Załóżmy, że f(f(a))=0.
Jednym z podstawień do danej równości będzie x=f(a).
29 cze 13:57
henrys: f(a)=−x
29 cze 16:07
henrys: a bardziej f(a)=−a

29 cze 16:08
AS: Rozwiązanie problemu 7
Niech A,B i C określają położenie środków okręgów.
Przyjąłem,że BC = a,AC = b,AB = c a promienie szukanych
okręgów r1 o środku w A,r2 o środku w B i r3 o środku w C.
Wtedy uzyskuję układ równań
r2 + r3 = a ,r1 + r3 = b , r1 + r2 = c
Dodając stronami mamy
2*r1 + 2*r2 + 2*r3 = a + b + c
r1 + r2 + r3 = 1/2(a + b + c) = m
lub
r1 + a = m => r1 = m − a
r2 + b = m => r2 = m − b
r3 + c = m => r3 = m − c
Konstrukcja
1. Na prostej odkładam kolejno odcinki a,b i c i połowię go (odcinek m)
2. Kolejno umniejszam odcinek m o a,b i c uzyskując pożądane
promienie r1,r2 i r3
3. Wystarczy teraz z punktów A,B i C zakreślić okręgi
30 cze 09:47
AS: Rozwiązanie problemu 8
b = 4√2 = √√2 = √a gdzie a = √2
Odcinek a znajduję kreśląc kwadrat o boku = 1,
przekątna tego kwadratu daje nam odcinek a.
Odcinek b znajduję następująco
Na prostej odkładam odcinek a i dołączam odcinek m = 1
uzyskując odcinek AB = a + m.
Wyznaczam środek S tego odcinka i promieniem SA
zakreślam półokrąg.
Z punktu wspólnego P odcinków a i m wykreślam prostopadłą
do przecięcia się z półokręgiem w punkcie R.
Odcinek PR jest rozwiązaniem.
30 cze 10:01
Eta:
Dla
AS .............

30 cze 11:36
anaisy: ok, jeszcze trochę i problem 6. będzie rozwiązany

.
30 cze 16:25
henrys: Problem 6
Niech x+f(x)=f(f(x)) dla każdego x∊R
Szukamy takiego a∊R, że f(f(a))=0, czyli szukamy miejsc zerowych funkcji f.
f(x
0)=0, x
0=f(a)
Podstawiamy do równania f(a)+f(f(a))=f(f(a)) ⇒f(a)=0. Dostajemy kolejne miejsce zerowe f ,
x
1=a. Znów podstawiamy do równania
a+0=0 ⇒ a=0.
Nie wiem czy ja nie spłaszczyłem tego problemu ale ruszmy coś

1 lip 11:44
abel:
f:R→R Rozważmy funkcję g:R2→R2
g(x,0)=(0,f(x))
Niech y=f(x) g(y,0)=(0,f(y)) z definicji funkcji f dla każdego x∊R zachodzi
g(f(x),0)=(0,f(f(x)))=(0,x+f(x)) ⇔f(x)=x+f(x)
⇔x=0, zatem tak zdefiniowana funkcja f nie istnieje.
1 lip 15:02
abel: glupoty pisze
1 lip 16:56
b.: @11:44: ,, Podstawiamy do równania f(a)+f(f(a))=f(f(a)) ⇒f(a)=0.''
Jeśli podstawiasz x=f(a), to po prawej powinno być f(f(f(a))) = f(0). Czyli dostajemy
f(a) + 0 = f(0).
Dalej f(f(0)) = f(f(a))=0, więc podstawiając x=0:
0 + f(0) = 0,
czyli f(0)=0. Stąd też f(a)=0.
Podstawiając x=a:
a + f(a) = f(f(a)), czyli a + 0 = 0.
Wobec tego jedynym możliwym a jest a=0.
Można by się zastanawiać, czy taka funkcja f w ogóle istnieje, choć do rozwiązania zadania nie
jest to konieczne.
1 lip 17:07
henryś: Masz rację, tam się machnąłem, ale to chyba nie jest dobre rozwiązanie.
1 lip 19:00
anaisy: abel z ostatniej Twojej równości wynika, że f(f(x))=x+f(x), nie f(x)=x+f(x). Taka funkcja
| | 1+√5 | |
istnieje np. f(x)= |
| x |
| | 2 | |
b. chodziło mi właśnie o takie rozwiązanie. Czekamy na 9. problem

.
1 lip 20:26
Mila:
Problem 9 (łatwy dla zachęty)
Dana jest funkcja:
f(x)=
√1+1x
| | 1 | | −1 | |
Rozwiąż równanie: f( |
| )= |
| |
| | x | | f'(1) | |
1 lip 20:52
anaisy: | | 1 | |
No to liczymy sobie pochodną f(x) i mamy f'(x)=− |
| , stąd |
| | 2x2√1+1x | |
| | −1 | | 1 | |
f'(1)= |
| , czyli chcemy rozwiązać równanie f( |
| )=2√2 ⇔ √1+x=2√2 |
| | 2√2 | | x | |
3 lip 15:49
anaisy: czyli x=7.
Na pewno o to chodziło?
3 lip 15:49
Dominik:
Źle policzona pochodna !
3 lip 16:45
Dominik:
Do tego brak dziedziny ! .... Twoja odp x= 7∉ D
Jak widać ... fajnie jest podawać kolejne "problemy" jak się zna sposób rozwiązania.
Gorzej gdy się nie zna rozwiązania.
Pozdrawiam

3 lip 16:50
Mila:
Dominik, przecież możesz podać swoją wersję.
Każdy z nas może się pomylić.
1) Pochodna obliczona prawidłowo, wynik prawidłowy.
2) Dziedzina f(x) :
x*(x+1)>0
x<−1 lub x>0
x∊(−
∞,−1)∪(0,
∞)
3) Dziedzina równania dla
Dominika zostaje.
3 lip 18:39
3 lip 18:50
Mila:
Anaisy, dobrze masz . Komentarz o pomyłce podałam w oderwaniu od Twojego rozwiązania.

3 lip 18:54
anaisy: Problem 10.
Startujemy od trójki liczb (1, 10, 100). W n−tym kroku możemy zamienić trójkę liczb (a, b, c)
| | a+b | | b+c | | c+a | |
na ( |
| , |
| , |
| ). Udowodnij, że po dowolnej liczbie ruchów (większej niż |
| | 2 | | 2 | | 2 | |
0) co najmniej jedna z liczb w otrzymanej trójce nie będzie całkowita.
3 lip 19:08
anaisy: Podpowiedź:
| | a+b | | b+c | | c+a | |
Załóżmy, że w trójce ( |
| , |
| , |
| )otrzymanej po pewnej liczbie ruchów |
| | 2 | | 2 | | 2 | |
wszystkie liczby są całkowite. Popatrzmy na różnicę dowolnych dwóch spośród tych liczb.
6 lip 15:38
anaisy: Ok, to skoro to zadanko Wam się nie spodobało, to pokażę rozwiązanie.
Załóżmy, że po n ruchach (ręcznie sprawdzamy, że n≥2) otrzymamy trójkę liczb całkowitych. Niech
| | x+y | | y+z | | z+x | |
(x, y, z) będzie trójką po (n−1)−tym ruchu. Wtedy liczby |
| , |
| , |
| są |
| | 2 | | 2 | | 2 | |
całkowite. Stąd wniosek, że liczba
jest całkowita. Analogicznie możemy pokazać, że liczby y i z są całkowite.
Mamy więc trójkę liczb całkowitych (x, y, z). Powtarzając rozumowanie pokazujemy, że po n−1,
n−2, ..., 1 mamy trójkę liczb całkowitych. Stąd wniosek, że liczby po pierwszym ruchu są
całkowite. Sprzeczność.
Problem 11.
Dane są liczby pierwsze p
1, p
2, ..., p
n, dla których
Udowodnij, że co najmniej dwie spośród liczb p
1, p
2, ..., p
n są równe.
7 lip 14:35
Kacper:
Myślę, że na początek wspólny mianownik

7 lip 14:40
b.: anaisy: ładne rozwiązanie, teraz zadanie (10) mi się już spodobało

7 lip 16:17
b.: OK, Kacper już podał rozwiązanie, ale nie zadanie, więc może się wtrące

Problem 11b. Czy istnieje rosnący ciąg liczb pierwszych p
1 < p
2 < ... taki, że
(Niestety, chyba nie jest to całkiem elementarne, raczej I rok studiów niż liceum).
7 lip 18:39
anaisy: b. No to pokaż rozwiązanie

.
15 lip 21:32
anaisy: No to może wrzucę następne zadanko, a
b. jak będzie na forum napisze coś o swoim

.
Problem 12.:
Rozwiąż układ równań w liczbach rzeczywistych:
(b+c+d)
4=3a
(c+d+a)
4=3b
(d+a+b)
4=3c
(a+b+c)
4=3d
16 lip 19:22
Vax: Zasada ekstremum
17 lip 00:55
anaisy: Nic się tutaj nie dzieje, więc wrzucam kolejne:
Problem 13.:
Udowodnij, że dla dowolnych liczb dodatnich a, b, c, zachodzi
| bc | | ca | | ab | | a+b+c | |
| + |
| + |
| ≤ |
| . |
| b+c | | c+a | | a+b | | 2 | |
20 wrz 16:19
Nuti: e, to na pewno z Cauchy'ego

20 wrz 16:27
anaisy: No to czekamy na rozwiązanie

.
20 wrz 16:35
ZKS:
| bc | | ac | | ab | | a + b + c | |
| + |
| + |
| ≤ |
| |
| b + c | | a + c | | b + c | | 2 | |
20 wrz 17:14
anaisy: Po rozwiązaniu zadanka wrzucamy (jedno) kolejne  !
!
−−
Ad. 13. Właśnie o takie rozwiązanie chodziło

.
21 wrz 14:46
przemek ania: siema co tam u ciebie słychac
21 wrz 17:01
przemek ania: ≤≤≤≤≤hej
21 wrz 17:07
PW: przemek ania, a gdy pójdziesz z pierwszą wizytą do rodziców narzeczonej, to koniecznie
nasraj w salonie.
21 wrz 17:23
Nuti: @PW
To Ty, czy ktoś Ciebie udaje? Srać w salonie

? A dlaczego akurat w salonie?
21 wrz 17:51
Metis: Nuti , przekaz niedosłowny

21 wrz 17:52
PW: Na ogół staram się dostosować przekaz do poziomu odbiorcy. Patrz, chyba zrozumiał, bo przestał
dopisywać głupoty przesuwające stare zadania do góry.
21 wrz 21:30
anaisy: No dobrze, to macie kolejne ode mnie.
Problem 14.
Dane są dwa ciągi liczb całkowitych dodatnich:
a
1, a
2, … , a
n
oraz
b
1, b
2, … , b
n
takie, że liczby a
i i b
i są względnie pierwsze dla wszystkich i ze zbioru {1, 2, …, n}.
Niech m oznacza najmniejszą wspólną wielokrotność liczb b
1, b
2, … , b
n.
Udowodnij, że
| | m | | m | | m | |
nwd(a1 |
| , a2 |
| , … , an |
| )=nwd(a1, a2, … , an) |
| | b1 | | b2 | | bn | |
Czekamy na rozwiązanie a
potem na kolejne zadanko.
29 wrz 16:11
TheCB: | | ai | |
Niech d=NWD(a1, a2, ..., an) oraz |
| =xi dla i∊{1, 2, ..., n}. Wówczas oczywiście |
| | d | |
mamy
NWD(x
1, x
2, ..., x
n)=1 oraz NWD(x
i, b
i)=1 dla i∊{1, 2, ..., n}. Pokażemy, że
| | m | | m | | m | |
NWD(x1 |
| , x2 |
| , ..., xn |
| )=1. Otóż załóżmy nie wprost, że istnieje |
| | b1 | | b2 | | n1 | |
liczba
pierwsza p, która jest wspólnym dzielnikiem liczb
| | m | | m | | m | |
x1 |
| , x2 |
| , ..., xn |
| . |
| | b1 | | b2 | | bn | |
Wówczas łatwo mamy p|x
1m, p|x
2m, ..., p|x
nm. Z faktu, że p jest liczbą pierwszą, wynika,
że albo p|x
1, p|x
2, ..., p|x
n, albo p|m. Pierwsza opcja jest jednak niemożliwa, ponieważ
mamy
NWD(x
1, x
2, ..., x
n)=1. Zatem p|m. Wiemy, że m=NWW(b
1, b
2, ..., b
n), a zatem istnieje
takie l∊{1, 2, ..., n}, że p|b
l. Niech k∊{1, 2, ..., n} będzie taką liczbą, dla której liczba
b
k w
rozkładzie na czynniki pierwsze ma przy p największy wykładnik spośród liczb
b
1, b
2, ..., b
n.
Oznaczmy ten wykładnik przez w. Wcześniej pokazaliśmy, że wykładnik ten wynosi co najmniej 1,
| | m | |
zatem p|bk. Wiemy, że NWD(bk, xk)=1, a zatem p nie dzieli xk. Jednak p|xk |
| , |
| | bk | |
| | m | |
skąd p| |
| . Z faktu, że pw|bk, wynika więc, że pw+1|m. Stąd jednak wynika, że wśród |
| | bk | |
liczb b
1, b
2, ..., b
n musi istnieć taka, która w rozkładzie na czynniki pierwsze ma przy p
wykładnik co najmniej w+1. Jednak najwyższym z tych wykładników jest w. Otrzymana
| | m | | m | | m | |
sprzeczność dowodzi, że rzeczywiście NWD(x1 |
| , x2 |
| , ..., xn |
| )=1. |
| | b1 | | b2 | | bn | |
Stąd mamy:
| | m | | m | | m | |
NWD(x1d |
| , x2d |
| , ..., xnd |
| )=d |
| | b1 | | b2 | | bn | |
| | m | | m | | m | |
NWD(a1 |
| , a2 |
| , ..., an |
| )=d=NWD(a1, a2, ..., an). |
| | b1 | | b2 | | bn | |
Co kończy dowód.
Problem 15.
Liczby a, b, c są liczbami rzeczywistymi dodatnimi, takimi, że abc=1. Udowodnij,
że a
2+b
2+c
2≥a+b+c.
2 maj 20:55
maturalna: a²+b²+c²+3>=2(a+b+c)
a(a−2)+b(b−2)+c(c−2)+3>=0
bo funkcja f(a)=a(a−2) ma najmiejszą wartość −1
Stąd i z nierówności miedzy srednią arytmetyczną i geometryczną
2a+2b+2c=a+b+c+a+b+c >=a+b+c +3 3√abc=a+b+c+3
Czyli udowodnilismy wyjściową nierówność.
Problem 16 (Zadanie maturalne)
Podano odległości a, b, c miedzy środkiem okręgu wpisanego i wierzchołkami trójkąta.
Oblicz promień r okręgu wpisanego, jeśli a= 1, b = 1/2, c = 1/3
2 maj 22:54
Jack: maturalna, skad nierorownosc
a2+b2+c2+3 ≥ 2(a+b+c) ?
2 maj 23:03
maturalna: Jak to skąd? Nie rozumiem pytania. Ta nierówność jest prawdziwa dla dowolnych a,b,c
:a2+b2+c2+3 ≥ 2(a+b+c), to pokazałam.
2 maj 23:12
Jack: kiedy to pokazalas? ; o
2 maj 23:14
maturalna: Na samym początku:
a²+b²+c²+3>=2(a+b+c)
a(a−2)+b(b−2)+c(c−2)+3>=0
bo funkcja f(a)=a(a−2) ma najmiejszą wartość −1
2 maj 23:15
Jack: hmm...sory ze ten tego...ale dlaczego akurat minimum to − 1?
2 maj 23:18
maturalna: f(a)=a(a−2) to funkcja kwadratowa o wierzchołku (1,−1)
2 maj 23:20
Jack: hmm...nie przekonuje mnie to, ale byc moze prawda... niech bedzie ; D
2 maj 23:21
maturalna: Ale co Cie nie przekonuje?
2 maj 23:23
Jack: taki zapis
a(a−2)+b(b−2)+c(c−2)+3>=0
nie mowie ze jest zly...bo moze byc poprawny ; D
2 maj 23:26
maturalna: Wg mnie jest dobrze jesli ktoś znajdzie błąd w moim rozumowaniu to nie bedzie obowiązyawało
moje zadani:
.
Problem 16 (Zadanie maturalne)
Podano odległości a, b, c miedzy środkiem okręgu wpisanego i wierzchołkami trójkąta.
Oblicz promień r okręgu wpisanego, jeśli a= 1, b = 1/2, c = 1/3
2 maj 23:28
3 maj 11:45
Przemysław: @yht
A Twoje zadanko?
4 maj 06:52
yht:
Niech a,b,c nalezą do rozwiązań |x2−3x+3|≤1 oraz
m,n należą do rozwiązań |x2−8x+9|≤ 4
tak że a+b+c+m+n=12
Znaleźć maksimum wyrazenia W=a*b*c*m*n
4 maj 08:14
b.: Dałem zadanie (7 lip 2015 18:39) i zapomniałem o tym.
Problem 11b. Czy istnieje rosnący ciąg liczb pierwszych p
1 < p
2 < ... taki, że
Odpowiedź: Tak.
W rozwiązaniu przydaje się wiedzieć, że szereg
gdzie q
n jest rosnącym ciągiem wszystkich liczb pierwszych, jest rozbieżny.
Określamy ciąg p
k z zadania następująco:
p
1 = 2,
jeśli mamy wybrane p
1, ..., p
n, to za p
n+1 bierzemy najmniejszą liczbę pierwszą > p
n
taką, żeby
| | 1 | | 1 | | 1 | |
|
| + |
| + ... + |
| < 1. |
| | p1 | | p2 | | pn+1 | |
W ten sposób wybierzemy nieskończony, rosnący ciąg liczb pierwszych.
Oczywiście wówczas
| 1 | | 1 | | 1 | |
| + |
| + ... + |
| + ... ≤ 1. |
| p1 | | p2 | | pn | |
| | 1 | | 1 | | 1 | |
Załóżmy nie wprost, że |
| + |
| + ... + |
| + ... = 1 − ε, gdzie ε>0. |
| | p1 | | p2 | | pn | |
| | 1 | |
Niech N będzie na tyle duże, że |
| < ε. |
| | pN | |
Jeśli jakaś z liczb pierwszych q > p
N nie zostałaby wybrana do ciągu (p
k), to oznaczałoby to
(ze sposobu wyboru tego ciągu), że
| | 1 | | 1 | | 1 | | 1 | |
A = ( |
| + |
| + ... + |
| + ... ) + |
| ≥ 1. |
| | p1 | | p2 | | pn | | pN | |
(Zamiast sumy nieskończonej można by nawet wziąć sumę skończoną po p
n < q).
Ale to jest niemożliwe, bo
| | 1 | | 1 | | 1 | | 1 | |
A = ( |
| + |
| + ... + |
| + ... ) + |
| < (1 − ε) + ε =1. |
| | p1 | | p2 | | pn | | pN | |
Zatem wszystkie liczby q > p
N występują w ciągu (p
k). Ale to też jest niemożliwe, bo szereg
gdzie sumowanie jest po liczbach pierwszych q, jest rozbieżny.
Wobec tego otrzymany ciąg (p
n) jest taki jak trzeba.
4 maj 17:28
TheCB: Zobaczymy, czy ktoś to jeszcze czyta

Zbiorem rozwiązań nierówności |x
2−3x+3|≤1 jest przedział [1, 2], a zbiorem rozwiązań
nierówności
|x
2−8x+9|≤ 4 − suma przedziałów [4 −
√11, 4 −
√3] i [4 +
√3, 4 +
√11]. Zaczniemy od
pokazania,
że wyrażenie W przyjmuje największą wartość, gdy a = b = c. Istotnie, załóżmy, że pewne dwie z
liczb
a, b, c są różne. Bez straty ogólności a ≠ b. Wówczas zamieniając parę (a, b) na parę
(
a+b2,
a+b2)
liczby stają się równe, nadal należą do przedziału [1, 2], ich suma się nie zmienia, a ich
iloczyn się zwiększa
(bo dla a ≠ b mamy
a+b2 >
√ab). Zatem przyjmijmy, że a = b = c. Wówczas 3a + m+ n = 12
W = a
3mn. Bez straty ogólności przyjmijmy, że m > n. Pokażemy, że m ∊ [4 +
√3, 4 +
√11]
i n ∊ [4 −
√11, 4 −
√3]. W tym celu zauważmy, że z tego, że a ∊ [1, 2] wynika, że
a ∊ (
4 − 2√33,
4 + 2√33), skąd po przekształceniach
12 − 3a2 ∊ (4 −
√3, 4
+
√3),
czyli
m + n2 ∊ (4 −
√3, 4 +
√3), co istotnie pokazuje, że liczby m i n nie mogą obie
należeć
do tego samego przedziału (spośród [4 +
√3, 4 +
√11] i [4 −
√11, 4 −
√3]) i w
konsekwencji
m ∊ [4 +
√3, 4 +
√11] i n ∊ [4 −
√11, 4 −
√3]. Pokażemy teraz, że
a ∊ [1,
4 + √11 − √33].
Istotnie, mamy 12 − 3a = m+n ≥ 4 −
√11 + 4 +
√3 = 8 −
√11 +
√3, skąd −3a ≥ −4 −
√11 +
√3
i w konsekwencji a ≤
4 + √11 − √33. Zatem a ∊ [1,
4 + √11 − √33]. Przyjmijmy
teraz,
że a jest pewną stałą. Na jej podstawie znajdziemy takie m, n , dla których m + n = 12 − 3a i
wartość
wyrażenia mn będzie największa z możliwych. Zauważmy, że 4mn = (m + n)
2 − (m − n)
2.
Oznacza to, że wartość wyrażenia mn będzie największa wtedy, gdy wartość wyrażenia |m − n| =
m − n będzie najmniejsza. Zauważmy, że póki liczby m − x, n + x (x > 0) należą odpowiednio
do przedziałów [4 +
√3, 4 +
√11] i [4 −
√11, 4 −
√3], to możemy nimi zastąpić liczby m,
n,
nie zmieniając przy tym ich sumy, a zmniejszając ich różnicę o 2x. Chcemy więc znaleźć
największe takie x, dla którego liczby te należą do odpowiednich przedziałów. Jeśli udałoby się
tak dobrać x, aby n + x = 4 −
√3 lub m − x = 4 +
√3, przy czym druga liczba pozostałaby
w odpowiednim przedziale, to byłby to wybór optymalny. Pokażemy, że zawsze da się tak zrobić
oraz
podamy, dla jakich a wystąpią poszczególne sytuacje. Przypuśćmy najpierw, że po zamianie
otrzymaliśmy
n = 4 −
√3. Wówczas m = 12 − 3a − (4 −
√3) = 8 − 3a +
√3. Nierówność m ≤ 4 +
√11
sprowadza
się do prawdziwej nierówności a ≥
4 + √3 − √113 (bo
4 + √3 − √113 < 1). Z
kolei nierówność
m ≥ 4 +
√3 sprowadza się do nierówności a ≤
43. Oznacza to, że przypadek ten ma miejsce,
gdy
a ∊ [1,
43]. Wówczas mamy W = a
3mn = a
3(4 −
√3)(8 − 3a +
√3). Szukamy
największej
możliwej wartości tego wyrażenia dla a ∊ [1,
43]. Zauważmy, że jest ona osiągana wtedy,
gdy
osiągana jest największa możliwa wartość wyrażenia a
3(8 − 3a +
√3) = −3a
4 + (8 +
√3)a
3.
Niech f(a) = −3a
4 + (8 +
√3)a
3. Wówczas f'(a) = −12a
3 + 3(8 +
√3)a
2. Jak łatwo
zauważyć,
pochodna f ma pierwiastek dwukrotny 0 oraz pierwiastek jednokrotny
8 + √34. Żadna z tych
liczb
nie należy do przedziału [1,
43], a zatem największa wartość f(a) w tym przedziale (a
zatem i W) jest
osiągana dla a = 1 lub a =
43. Mamy f(1) = 5 +
√3 oraz f(
43) = (
43)
3(4 +
√3) =
64(4 + √3)27 > 2(4 +
√3) > 5 +
√3. Zatem w tym przypadku największa możliwa wartość
wyrażenia W
wynosi
64(4 + √3)(4 − √3)27 =
83227. Pozostało rozpatrzeć przypadek, w którym po
zamianie
otrzymalibyśmy m = 4 +
√3. Wówczas n = 8 − 3a −
√3. Nierówność n ≥ 4 −
√11 sprowadza się
do prawdziwej
nierówności a ≤
4 + √11 − √33, a nierówność n ≤ 4 −
√3 sprowadza się do nierówności
a ≥
43.
Oznacza to, że ten przypadek ma miejsce, gdy a ∊ [
43,
4 + √11 − √33] (dla a =
43 możemy
otrzymać m = 4 +
√3 i n = 4 −
√3). Wówczas W = a
3(4 +
√3)(8 − 3a −
√3). Szukamy
największej
możliwej wartości tego wyrażenia dla a ∊ [
43,
4 + √11 − √33]. Zauważmy, że jest
ona osiągana
wtedy, gdy osiągana jest największa możliwa wartość wyrażenia a
3(8 − 3a −
√3) = −3a
4 +
(8 −
√3)a
3.
Niech g(a) = −3a
4 + (8 −
√3)a
3. Wówczas g'(a) = −12a
3 + 3(8 −
√3)a
2. Jak łatwo
zauważyć,
pochodna g ma pierwiastek dwukrotny a = 0 i pierwiastek jednokrotny
8 − √34. Stąd łatwo
wynika,
że funkcja f osiąga maksimum dla argumentu a =
8 − √34. Zauważmy, że argument ten należy
do przedziału [
43,
4 + √11 − √33]. Oznacza to, że wyrażenie W w tym przypadku
osiągnie
maksimum dla a =
8 − √34. Wynosi ono wówczas (po przekształceniach, nie będę tego
przepisywał,
bo jest tam trochę liczenia)
14596 − 3319√3256. Nietrudno zauważyć, że liczba ta jest
większa niż
83227 (choć też trochę trzeba policzyć). Oznacza to, że szukaną największą wartością
wyrażenia W
jest
14596 − 3319√3256 i jest ona osiągana dla a = b = c = n =
8 − √34 i m = 4 +
√3.
Problem 18.
Styczne do okręgu ω w punktach A i B przecinają się w punkcie P. Punkt M jest środkiem odcinka
AP, punkt N zaś drugim punktem przecięcia prostej BM z okręgiem ω. Wykaż, że PN = 2MN.
11 lip 18:32
TheCB: Hint: Rozważ punkt symetryczny do N względem punktu M.
25 lip 18:39
kos: TheCB polesiałes......

Oznaczmy ten punkt N' wtedy na czworokącie N"ABP można opisać okrąg?
26 lip 01:42
TheCB: Jak najbardziej. Wrzucaj zadanie (hint tak dużo dawał, bo chciałem uaktywnić trochę temat).
26 lip 21:58
kos: Nie mam trudnychale niech bedzie to ale z rozwiązaniem do końca, nie tylko podanie warunków:
Problem 19
Wyznacz parametr a tak aby równanie log( x2 + 2ax) − log( 8x − 6a − 3) = 0 miało tylko jedno
rozwiązanie.
26 lip 22:18
26 lip 22:49
kos: Ale napisałem zeby rozwiazć do końca moje...
27 lip 08:27
TheCB: Dobra, podejmę się spisywania tego. Mamy log( x
2 + 2ax) = log(8x − 6a − 3). Funkcja
logarytmiczna jest różnowartościowa, więc musi zachodzić równość x
2 + 2ax = 8x − 6a − 3.
Chcemy znaleźć takie wartości parametru a, aby równanie to miało tylko jedno rozwiązanie
spełniające 8x > 6a + 3. Mamy x
2 + (2a − 8)x + (6a + 3) = 0.
Liczymy deltę i otrzymujemy Δ = (2a − 8)
2 − 4(6a + 3) = 4a
2 − 56a + 52 = 4(a
2 − 14a +
13).
Oczywiście musi zachodzić Δ ≥ 0, skąd a
2 − 14a + 13 ≥ 0. Rozwiązaniami tej nierówności jest
suma
przedziałów (−
∞, 1] oraz [13,
∞). Jeśli a = 13, to mamy (x + 9)
2 = 0, skąd x = −9. Wówczas
jednak
8x < 6a + 3. Jeśli a = 1, to mamy (x − 3)
2 = 0, skąd x = 3 i wówczas istotnie 8x > 6a + 3.
Załóżmy
teraz, że a ∊ (−
∞, 1) ∪ (13,
∞). Wówczas równanie x
2 + (2a − 8)x + (6a + 3) = 0 ma dwa
rozwiązania:
| (8 − 2a − 2√a2 − 14a + 13) | |
| = 4 − a − √a2 − 14a + 13 oraz 4 − a + √a2 − 14a + 13. |
| 2 | |
Oczywiście
4 − a +
√a2 − 14a + 13 > 4 − a −
√a2 − 14a + 13, a zatem musi zachodzić 4 − a +
√a2 −
14a + 13 >
6a + 38
oraz 4 − a −
√a2 − 14a + 13 ≤
6a + 38. Z pierwszej nierówności mamy:
8
√a2 − 14a + 13 > 14a − 29
64(a
2 − 14a + 13) > 196a
2 − 812a + 841
−132a
2 − 84a − 9 > 0
132a
2 + 84a + 9 < 0
44a
2 + 28a + 3 < 0
44(a +
12)(a +
322) < 0
(a +
12)(a +
322) < 0.
Stąd łatwo a ∊ (
322,
12). Oczywiście przedział ten zawiera się we wcześniej
wspomnianej sumie przedziałów.
Nietrudno jednak zauważyć, że druga nierówność prowadzi do nierówności 8
√a2 − 14a + 13 ≥ 14a
− 29, która zachodzi dla wyznaczonych wcześniej a. To oznacza, że a = 1 lub a ∊ (
322,
12).
Miejmy nadzieję, że nie walnąłem się w obliczeniach.
Problem 20.
Punkt N leży na boku BC trójkąta ABC, a punkt P − na odcinku AN. Wiadomo, że zachodzą równości:
∡ANB = 90°
∡PBA = 20°
∡PBC = 40°
∡PCB = 30°.
Wyznacz miarę kąta ∡PCA.
27 lip 16:18
kos: Oj trochę się pomyliłeś przy rozwiązywaniu nierównośći kwdratowej

27 lip 16:32
TheCB: Możliwe, gdzie?
27 lip 16:53
kos: a jak się rozwiązuje (a+1/2)(a+3/22)<0

mlutki błędzik

27 lip 17:20
TheCB: Faktycznie, mózg mi się wyłączył. Ma być oczywiście a ∊ (−12, −322). Ostateczna
odpowiedź to zatem a = 1 oraz a ∊ (−12, −322).
27 lip 17:26
kos: a co z końcami tego przedziału

27 lip 17:34
Jula: Punkt P punkt przecięcia wysokosci.
29 lip 12:34
anaisy: To może pełne rozwiązanie zadanka 20.:
Załóżmy, że CP, AB przecinają się w C1, a BP, AC w B1.
Kąty C1BC i C1CB sumują się do 90 st, więc AB i CP są prostopadłe. Skoro wysokości trójkąta
przecinają się w jednym punkcie to P jest ortocentrum ABC. Czyli kąty BC1C, BB1C są proste,
więc na BCB1C1 można opisać okrąg. W tym okręgu kąty C1BB1 i C1CB1 są oparte na tym
samym łuku, czyli miara kąta C1CB1 jest równa 20 st.
Problem 21.
Dane są parami różne liczby pierwsze p1, p2, ..., pn, których suma odwrotności jest równa
odwrotności pewnej liczby naturalnej. Udowodnij, że n=1.
20 maj 15:31
Adamm:
1/p
1+...+1/p
n=1/k, k∊N
| | p1...pn | |
k= |
| |
| | ∑i=1n ∏1≤j≤n, j≠i pj | |
o ile tylko n≥2 to mianownik nie jest podzielny przez p
i dla 1≤i≤n
ale licznik tak, skąd wniosek że p
1...p
n|k
co jest sprzeczne bo, p
1...p
n>k
20 maj 15:55
Adamm:
Może coś takiego?
Problem 22.
Udowodnić że liczba powstała przez wypisywanie kolejnych liczb naturalnych, to jest
0,12345678910111213..., jest niewymierna
20 maj 16:34
Basia: dowód nie wprost
przypuśćmy, że ta liczba jest wymierna
musi mieć w takim razie:
1. rozwinięcie dziesietne skończone ⇒ w zbiorze N istnieje liczba największa
sprzeczność
2. rozwinięcie nieskończone okresowe (okres jest liczbą skończoną c
1c
2...c
n) ⇒
w zbiorze N istnieje liczba największa
sprzeczność
Problem 23
Udowodnić, że każda liczba wymierna ma rozwinięcie dziesiętne skończone lub nieskończone
okresowe.
(to łatwe, ale na razie nic mądrzejszego mi do głowy nie przyszło)

21 maj 04:49
Adamm:
Basia, pierwszy podpunkt mogę uwierzyć na słowo, ale drugi to już musisz wyjaśnić
21 maj 15:20
r0bert: hej! a może coś z realnego świata? Wilgotność względna na zewnątrz 92% temperatura
12oC=wilgotność bezwzględna a=9,9 g/m∧3. W mieszkaniu mam niezmiennie f=65% wilgoci i je
wietrze oraz schładzam. To na jakiej temperaturze zatrzymać klimatyzator by nie wpuszczać
wilgoci z zewnątrz? Łatwiejszy wzór Tetensa, szukane w obu przypadkach T=?
100a/(0,8f)*(1+(1/273)T)=6,11*10∧(7,5T/(237,3+T))
wg. trudniejszego wzoru Bucka:
100a/(0,8f)*(1+(1/273)T)=6,1121*e∧((18,678−T/234,5)*(T/(257,14+T)))
Ja tego nie przekształcę bo po wielu latach zapomniałem, ale jak ktoś zrobi to mi się przyda.
Excel podaje przybliżoną wartość T ok. 17±18 oC.
23 maj 04:06
ford:
ze wzoru typu aT+b+cT=0 nie wyznaczysz analitycznie T, zostają metody przybliżone
23 maj 06:40
fuerta:
15 kwi 11:33
ite:
@fuerta czy to jest zachęta do wstawiania zadań maturalnych do poćwiczenia?
15 kwi 12:55
fuerta: Tak

ale takie maturalne a nie konkursowe
15 kwi 12:59
ite: a poprawiasz wynik?
15 kwi 13:00
ite: Najlepiej załóż nowy wątek i podaj, czy to mają być zadania z rozszerzenia.
15 kwi 13:06
 (chyba, że znajdzie się coś wyjątkowo
trudnego, wtedy fajnie będzie jeśli autor po pewnym czasie poda swoje rozwiązanie lub
wskazówki).
To na początek coś takiego:
Problem 1.:
Niech D będzie spodkiem wysokości poprowadzonej z wierzchołka A w trójkącie ABC. Rozważmy
punkty E i F leżące odpowiednio na odcinkach AB i AC takie że proste AB i DE oraz proste CA i
DF są prostopadłe. Udowodnij, że punkty B, C, F, E leżą na jednym okręgu.
(chyba, że znajdzie się coś wyjątkowo
trudnego, wtedy fajnie będzie jeśli autor po pewnym czasie poda swoje rozwiązanie lub
wskazówki).
To na początek coś takiego:
Problem 1.:
Niech D będzie spodkiem wysokości poprowadzonej z wierzchołka A w trójkącie ABC. Rozważmy
punkty E i F leżące odpowiednio na odcinkach AB i AC takie że proste AB i DE oraz proste CA i
DF są prostopadłe. Udowodnij, że punkty B, C, F, E leżą na jednym okręgu.



 Dlaczego tak bardzo na liczenie
Dlaczego tak bardzo na liczenie ?
No ale dobra. Załóżmy sobie że te proste to k i l, punkty B, C leżą na prostej l a punkty B' C'
na prostej k. Na początku rozważymy przypadek w którym A leży na k (wtedy a pokrywa się z B' i
z C'). Zastanówmy się jakie będą długości odcinków AB i AC (b.s.o AB>AC), gdy ∡BAC=120[deg].
Niech AB=x, AC=y i BC=z. Wystarczy, że rozwiążemy układ równań:
x+y=5
?
No ale dobra. Załóżmy sobie że te proste to k i l, punkty B, C leżą na prostej l a punkty B' C'
na prostej k. Na początku rozważymy przypadek w którym A leży na k (wtedy a pokrywa się z B' i
z C'). Zastanówmy się jakie będą długości odcinków AB i AC (b.s.o AB>AC), gdy ∡BAC=120[deg].
Niech AB=x, AC=y i BC=z. Wystarczy, że rozwiążemy układ równań:
x+y=5
 1. Nie rozumiem treści zarzutu ani kto je postawił.
2. Nigdzie nie znalazłem regulaminu który by tę sprawę regulował.
3. Jeżeli już problem znalazł się na Forum to proponuję swoje
rozwiązanie
4. Amen
1 x + y = 120o
2. BB1 = h/cos(x) , CC1 = h/cos(y)
Z warunku postawionym w zadaniu zachodzi
h/cos(x) + h/cos(y) = m
Do rozwiązania równanie
h*cos(y) + h*cos(x) = m*cos(x)*cos(y)
Po podstawieniu h i m mamy
cos(y) + cos(x) = 5*cosx*cos(y)
1. Nie rozumiem treści zarzutu ani kto je postawił.
2. Nigdzie nie znalazłem regulaminu który by tę sprawę regulował.
3. Jeżeli już problem znalazł się na Forum to proponuję swoje
rozwiązanie
4. Amen
1 x + y = 120o
2. BB1 = h/cos(x) , CC1 = h/cos(y)
Z warunku postawionym w zadaniu zachodzi
h/cos(x) + h/cos(y) = m
Do rozwiązania równanie
h*cos(y) + h*cos(x) = m*cos(x)*cos(y)
Po podstawieniu h i m mamy
cos(y) + cos(x) = 5*cosx*cos(y)
 .
.
 ?
?
 Jeżeli punkty A,B,E,F leżą na okręgu , to czworokąt ABEF jest wpisany w okrąg,
to z warunku wpisania czworokąta w okrąg mamy:
β+90o+α=180o ⇒ α+β= 90o i γ+90o+δ=180o ⇒ γ+δ= 90o
Taka zależność między kątami zachodzi
bo DC jest wysokością opuszczoną na bok AB
to |∡ADC|= 90o= α+β i |∡BDC|= γ+δ= 90o
zatem punkty A,B, E, F , leżą na jednym okręgu
c.n.u
Jeżeli punkty A,B,E,F leżą na okręgu , to czworokąt ABEF jest wpisany w okrąg,
to z warunku wpisania czworokąta w okrąg mamy:
β+90o+α=180o ⇒ α+β= 90o i γ+90o+δ=180o ⇒ γ+δ= 90o
Taka zależność między kątami zachodzi
bo DC jest wysokością opuszczoną na bok AB
to |∡ADC|= 90o= α+β i |∡BDC|= γ+δ= 90o
zatem punkty A,B, E, F , leżą na jednym okręgu
c.n.u
 ):
No to wyrażenie
):
No to wyrażenie

 .
.

 .
Rozwiązanie problemu 4.:
Rozumiem, że ten punkt może znajdować się też na boku tego pięciokąta? (inaczej nie działa dla
pięciokąta (0,0), (2,0), (2,1), (1, 2), (0,1).
Załóżmy, że mamy pięciokąt A1A2A3A4A5, przy czym jego wierzchołki mają odpowiednio
współrzędne Ak=(xk, yk) dla k∊[1,5]
Załóżmy, że wewnątrz pięciokąta nie istnieje żaden punkt. To oznacza, że |xn−xm|<2 (1) oraz
|yn−ym|<2 (2)dla dowolnych n,m∊[1,5]. Z zasady szufladkowej Dirichleta mamy, że istnieje
taki zbiór trzech wierzchołków (niekoniecznie kolejnych) danego pięciokąta
{X1, X2, X3}⊂{A1, A2, ... , A5}
że X1=(a1, b1), X2=(a2, b2), X3=(a3, b3) oraz a1≡a2≡a3 (mod 2), zatem z nierówności
(1) wynika, że a1=a2=a3. Ponadto z zasady szufladkowej Dirichleta wynika, że dwie spośród
liczb b1, b2, b3 mają tę samą parzystość, załóżmy baz straty ogólności, że b1 i b2.
Analogicznie mamy b1=b2 lub |b1−b2|≥2, zatem z (2) mamy b1 =b2. Stąd wniosek, że punkty
X1 i X2 się pokrywają, zatem sprzeczność, zatem conajmniej jedna z nierówności (1), (2) jest
nieprawdziwa, co kończy dowód.
___________
Zaraz znajdę następne zadanko.
.
Rozwiązanie problemu 4.:
Rozumiem, że ten punkt może znajdować się też na boku tego pięciokąta? (inaczej nie działa dla
pięciokąta (0,0), (2,0), (2,1), (1, 2), (0,1).
Załóżmy, że mamy pięciokąt A1A2A3A4A5, przy czym jego wierzchołki mają odpowiednio
współrzędne Ak=(xk, yk) dla k∊[1,5]
Załóżmy, że wewnątrz pięciokąta nie istnieje żaden punkt. To oznacza, że |xn−xm|<2 (1) oraz
|yn−ym|<2 (2)dla dowolnych n,m∊[1,5]. Z zasady szufladkowej Dirichleta mamy, że istnieje
taki zbiór trzech wierzchołków (niekoniecznie kolejnych) danego pięciokąta
{X1, X2, X3}⊂{A1, A2, ... , A5}
że X1=(a1, b1), X2=(a2, b2), X3=(a3, b3) oraz a1≡a2≡a3 (mod 2), zatem z nierówności
(1) wynika, że a1=a2=a3. Ponadto z zasady szufladkowej Dirichleta wynika, że dwie spośród
liczb b1, b2, b3 mają tę samą parzystość, załóżmy baz straty ogólności, że b1 i b2.
Analogicznie mamy b1=b2 lub |b1−b2|≥2, zatem z (2) mamy b1 =b2. Stąd wniosek, że punkty
X1 i X2 się pokrywają, zatem sprzeczność, zatem conajmniej jedna z nierówności (1), (2) jest
nieprawdziwa, co kończy dowód.
___________
Zaraz znajdę następne zadanko.
 Nie na boku tylko wewnątrz
Nie na boku tylko wewnątrz 


 Proponuję takie rozwiązanie problemu 4.
Zacznę od analizy
Niech ΔABC będzie szukanym trójkątem.
Odkładając odcinek DA = AC i EB = BC na prostej DE
mamy odcinek DE = m , trójkąty DAC i EBC są równoramienne
a kąty odpowiednio równe kąt m = α/2 i kąt n = β/2
Już staje się jasne jak poprowadzić konstrukcję.
Rozwiązanie
1. Na prostej odłożyć odcinek DE = m
2.Przy punkcie D odłożyć kąt ADC = α/2 a przy punkcie E kąt β/2
3.Ramiona tych kątów w przecięciu wyznaczą punkt C
4.Przy punkcie C odkładamy kąt DCA = α/2 i kąt ECB = β/2
5. Ramiona tych kątów wyznaczą szukane punkty A i B.
6. W ten sposób uzyskaliśmy szukany trójkąt ABC
Proponuję takie rozwiązanie problemu 4.
Zacznę od analizy
Niech ΔABC będzie szukanym trójkątem.
Odkładając odcinek DA = AC i EB = BC na prostej DE
mamy odcinek DE = m , trójkąty DAC i EBC są równoramienne
a kąty odpowiednio równe kąt m = α/2 i kąt n = β/2
Już staje się jasne jak poprowadzić konstrukcję.
Rozwiązanie
1. Na prostej odłożyć odcinek DE = m
2.Przy punkcie D odłożyć kąt ADC = α/2 a przy punkcie E kąt β/2
3.Ramiona tych kątów w przecięciu wyznaczą punkt C
4.Przy punkcie C odkładamy kąt DCA = α/2 i kąt ECB = β/2
5. Ramiona tych kątów wyznaczą szukane punkty A i B.
6. W ten sposób uzyskaliśmy szukany trójkąt ABC
 . Aktualny
jest problem 6.
. Aktualny
jest problem 6.
 Zadanie jest po to, by Inni ( jak tu zajrzą) też to wiedzieli.
Zadanie jest po to, by Inni ( jak tu zajrzą) też to wiedzieli.


 .
.

 .
.




 Problem 11b. Czy istnieje rosnący ciąg liczb pierwszych p1 < p2 < ... taki, że
Problem 11b. Czy istnieje rosnący ciąg liczb pierwszych p1 < p2 < ... taki, że
 .
.
 .
Problem 12.:
Rozwiąż układ równań w liczbach rzeczywistych:
(b+c+d)4=3a
(c+d+a)4=3b
(d+a+b)4=3c
(a+b+c)4=3d
.
Problem 12.:
Rozwiąż układ równań w liczbach rzeczywistych:
(b+c+d)4=3a
(c+d+a)4=3b
(d+a+b)4=3c
(a+b+c)4=3d

 .
.
 !
−−
Ad. 13. Właśnie o takie rozwiązanie chodziło
!
−−
Ad. 13. Właśnie o takie rozwiązanie chodziło  .
.
 ? A dlaczego akurat w salonie?
? A dlaczego akurat w salonie?

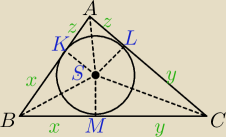 AS = 1/3
BS = 1/2
CS = 1
KS=LS=MS = r
z pitagorasów w trójkątach AKS, KSB, SMC masz równania:
z2+r2=1/9 → z=√1/9−r2
x2+r2=1/4 → x=√1/4−r2
y2+r2=1 → y=√1−r2
CS − dwusieczna kąta MCL, stąd ∡MCS=∡LCS, ∡MCL=2∡MCS
w trójkątach prostokątnych MCS i LCS:
sin(∡MCS) = sin(∡LCS) = r
cos(∡MCS) = cos(∡LCS) = y
sin(∡MCL) = sin(2∡MCS)=2sin(∡MCS)*cos(∡MCS) = 2*r*y
ze wzoru na pole trójkąta P=p*r wynika, że P=(x+y+z)*r
AS = 1/3
BS = 1/2
CS = 1
KS=LS=MS = r
z pitagorasów w trójkątach AKS, KSB, SMC masz równania:
z2+r2=1/9 → z=√1/9−r2
x2+r2=1/4 → x=√1/4−r2
y2+r2=1 → y=√1−r2
CS − dwusieczna kąta MCL, stąd ∡MCS=∡LCS, ∡MCL=2∡MCS
w trójkątach prostokątnych MCS i LCS:
sin(∡MCS) = sin(∡LCS) = r
cos(∡MCS) = cos(∡LCS) = y
sin(∡MCL) = sin(2∡MCS)=2sin(∡MCS)*cos(∡MCS) = 2*r*y
ze wzoru na pole trójkąta P=p*r wynika, że P=(x+y+z)*r
 Zbiorem rozwiązań nierówności |x2−3x+3|≤1 jest przedział [1, 2], a zbiorem rozwiązań
nierówności
|x2−8x+9|≤ 4 − suma przedziałów [4 − √11, 4 − √3] i [4 + √3, 4 + √11]. Zaczniemy od
pokazania,
że wyrażenie W przyjmuje największą wartość, gdy a = b = c. Istotnie, załóżmy, że pewne dwie z
liczb
a, b, c są różne. Bez straty ogólności a ≠ b. Wówczas zamieniając parę (a, b) na parę
(a+b2, a+b2)
liczby stają się równe, nadal należą do przedziału [1, 2], ich suma się nie zmienia, a ich
iloczyn się zwiększa
(bo dla a ≠ b mamy a+b2 > √ab). Zatem przyjmijmy, że a = b = c. Wówczas 3a + m+ n = 12
W = a3mn. Bez straty ogólności przyjmijmy, że m > n. Pokażemy, że m ∊ [4 + √3, 4 + √11]
i n ∊ [4 − √11, 4 − √3]. W tym celu zauważmy, że z tego, że a ∊ [1, 2] wynika, że
a ∊ (4 − 2√33, 4 + 2√33), skąd po przekształceniach 12 − 3a2 ∊ (4 − √3, 4
+ √3),
czyli m + n2 ∊ (4 − √3, 4 + √3), co istotnie pokazuje, że liczby m i n nie mogą obie
należeć
do tego samego przedziału (spośród [4 + √3, 4 + √11] i [4 − √11, 4 − √3]) i w
konsekwencji
m ∊ [4 + √3, 4 + √11] i n ∊ [4 − √11, 4 − √3]. Pokażemy teraz, że
a ∊ [1, 4 + √11 − √33].
Istotnie, mamy 12 − 3a = m+n ≥ 4 − √11 + 4 + √3 = 8 − √11 + √3, skąd −3a ≥ −4 − √11 +
√3
i w konsekwencji a ≤ 4 + √11 − √33. Zatem a ∊ [1, 4 + √11 − √33]. Przyjmijmy
teraz,
że a jest pewną stałą. Na jej podstawie znajdziemy takie m, n , dla których m + n = 12 − 3a i
wartość
wyrażenia mn będzie największa z możliwych. Zauważmy, że 4mn = (m + n)2 − (m − n)2.
Oznacza to, że wartość wyrażenia mn będzie największa wtedy, gdy wartość wyrażenia |m − n| =
m − n będzie najmniejsza. Zauważmy, że póki liczby m − x, n + x (x > 0) należą odpowiednio
do przedziałów [4 + √3, 4 + √11] i [4 − √11, 4 − √3], to możemy nimi zastąpić liczby m,
n,
nie zmieniając przy tym ich sumy, a zmniejszając ich różnicę o 2x. Chcemy więc znaleźć
największe takie x, dla którego liczby te należą do odpowiednich przedziałów. Jeśli udałoby się
tak dobrać x, aby n + x = 4 − √3 lub m − x = 4 + √3, przy czym druga liczba pozostałaby
w odpowiednim przedziale, to byłby to wybór optymalny. Pokażemy, że zawsze da się tak zrobić
oraz
podamy, dla jakich a wystąpią poszczególne sytuacje. Przypuśćmy najpierw, że po zamianie
otrzymaliśmy
n = 4 − √3. Wówczas m = 12 − 3a − (4 − √3) = 8 − 3a + √3. Nierówność m ≤ 4 + √11
sprowadza
się do prawdziwej nierówności a ≥ 4 + √3 − √113 (bo 4 + √3 − √113 < 1). Z
kolei nierówność
m ≥ 4 + √3 sprowadza się do nierówności a ≤ 43. Oznacza to, że przypadek ten ma miejsce,
gdy
a ∊ [1, 43]. Wówczas mamy W = a3mn = a3(4 − √3)(8 − 3a + √3). Szukamy
największej
możliwej wartości tego wyrażenia dla a ∊ [1, 43]. Zauważmy, że jest ona osiągana wtedy,
gdy
osiągana jest największa możliwa wartość wyrażenia a3(8 − 3a + √3) = −3a4 + (8 +
√3)a3.
Niech f(a) = −3a4 + (8 + √3)a3. Wówczas f'(a) = −12a3 + 3(8 + √3)a2. Jak łatwo
zauważyć,
pochodna f ma pierwiastek dwukrotny 0 oraz pierwiastek jednokrotny 8 + √34. Żadna z tych
liczb
nie należy do przedziału [1, 43], a zatem największa wartość f(a) w tym przedziale (a
zatem i W) jest
osiągana dla a = 1 lub a = 43. Mamy f(1) = 5 + √3 oraz f(43) = (43)3(4 +
√3) =
64(4 + √3)27 > 2(4 + √3) > 5 + √3. Zatem w tym przypadku największa możliwa wartość
wyrażenia W
wynosi 64(4 + √3)(4 − √3)27 = 83227. Pozostało rozpatrzeć przypadek, w którym po
zamianie
otrzymalibyśmy m = 4 + √3. Wówczas n = 8 − 3a − √3. Nierówność n ≥ 4 − √11 sprowadza się
do prawdziwej
nierówności a ≤ 4 + √11 − √33, a nierówność n ≤ 4 − √3 sprowadza się do nierówności
a ≥ 43.
Oznacza to, że ten przypadek ma miejsce, gdy a ∊ [43, 4 + √11 − √33] (dla a =
43 możemy
otrzymać m = 4 + √3 i n = 4 − √3). Wówczas W = a3(4 + √3)(8 − 3a − √3). Szukamy
największej
możliwej wartości tego wyrażenia dla a ∊ [43, 4 + √11 − √33]. Zauważmy, że jest
ona osiągana
wtedy, gdy osiągana jest największa możliwa wartość wyrażenia a3(8 − 3a − √3) = −3a4 +
(8 − √3)a3.
Niech g(a) = −3a4 + (8 − √3)a3. Wówczas g'(a) = −12a3 + 3(8 − √3)a2. Jak łatwo
zauważyć,
pochodna g ma pierwiastek dwukrotny a = 0 i pierwiastek jednokrotny 8 − √34. Stąd łatwo
wynika,
że funkcja f osiąga maksimum dla argumentu a = 8 − √34. Zauważmy, że argument ten należy
do przedziału [43, 4 + √11 − √33]. Oznacza to, że wyrażenie W w tym przypadku
osiągnie
maksimum dla a = 8 − √34. Wynosi ono wówczas (po przekształceniach, nie będę tego
przepisywał,
bo jest tam trochę liczenia) 14596 − 3319√3256. Nietrudno zauważyć, że liczba ta jest
większa niż
83227 (choć też trochę trzeba policzyć). Oznacza to, że szukaną największą wartością
wyrażenia W
jest 14596 − 3319√3256 i jest ona osiągana dla a = b = c = n = 8 − √34 i m = 4 +
√3.
Problem 18.
Styczne do okręgu ω w punktach A i B przecinają się w punkcie P. Punkt M jest środkiem odcinka
AP, punkt N zaś drugim punktem przecięcia prostej BM z okręgiem ω. Wykaż, że PN = 2MN.
Zbiorem rozwiązań nierówności |x2−3x+3|≤1 jest przedział [1, 2], a zbiorem rozwiązań
nierówności
|x2−8x+9|≤ 4 − suma przedziałów [4 − √11, 4 − √3] i [4 + √3, 4 + √11]. Zaczniemy od
pokazania,
że wyrażenie W przyjmuje największą wartość, gdy a = b = c. Istotnie, załóżmy, że pewne dwie z
liczb
a, b, c są różne. Bez straty ogólności a ≠ b. Wówczas zamieniając parę (a, b) na parę
(a+b2, a+b2)
liczby stają się równe, nadal należą do przedziału [1, 2], ich suma się nie zmienia, a ich
iloczyn się zwiększa
(bo dla a ≠ b mamy a+b2 > √ab). Zatem przyjmijmy, że a = b = c. Wówczas 3a + m+ n = 12
W = a3mn. Bez straty ogólności przyjmijmy, że m > n. Pokażemy, że m ∊ [4 + √3, 4 + √11]
i n ∊ [4 − √11, 4 − √3]. W tym celu zauważmy, że z tego, że a ∊ [1, 2] wynika, że
a ∊ (4 − 2√33, 4 + 2√33), skąd po przekształceniach 12 − 3a2 ∊ (4 − √3, 4
+ √3),
czyli m + n2 ∊ (4 − √3, 4 + √3), co istotnie pokazuje, że liczby m i n nie mogą obie
należeć
do tego samego przedziału (spośród [4 + √3, 4 + √11] i [4 − √11, 4 − √3]) i w
konsekwencji
m ∊ [4 + √3, 4 + √11] i n ∊ [4 − √11, 4 − √3]. Pokażemy teraz, że
a ∊ [1, 4 + √11 − √33].
Istotnie, mamy 12 − 3a = m+n ≥ 4 − √11 + 4 + √3 = 8 − √11 + √3, skąd −3a ≥ −4 − √11 +
√3
i w konsekwencji a ≤ 4 + √11 − √33. Zatem a ∊ [1, 4 + √11 − √33]. Przyjmijmy
teraz,
że a jest pewną stałą. Na jej podstawie znajdziemy takie m, n , dla których m + n = 12 − 3a i
wartość
wyrażenia mn będzie największa z możliwych. Zauważmy, że 4mn = (m + n)2 − (m − n)2.
Oznacza to, że wartość wyrażenia mn będzie największa wtedy, gdy wartość wyrażenia |m − n| =
m − n będzie najmniejsza. Zauważmy, że póki liczby m − x, n + x (x > 0) należą odpowiednio
do przedziałów [4 + √3, 4 + √11] i [4 − √11, 4 − √3], to możemy nimi zastąpić liczby m,
n,
nie zmieniając przy tym ich sumy, a zmniejszając ich różnicę o 2x. Chcemy więc znaleźć
największe takie x, dla którego liczby te należą do odpowiednich przedziałów. Jeśli udałoby się
tak dobrać x, aby n + x = 4 − √3 lub m − x = 4 + √3, przy czym druga liczba pozostałaby
w odpowiednim przedziale, to byłby to wybór optymalny. Pokażemy, że zawsze da się tak zrobić
oraz
podamy, dla jakich a wystąpią poszczególne sytuacje. Przypuśćmy najpierw, że po zamianie
otrzymaliśmy
n = 4 − √3. Wówczas m = 12 − 3a − (4 − √3) = 8 − 3a + √3. Nierówność m ≤ 4 + √11
sprowadza
się do prawdziwej nierówności a ≥ 4 + √3 − √113 (bo 4 + √3 − √113 < 1). Z
kolei nierówność
m ≥ 4 + √3 sprowadza się do nierówności a ≤ 43. Oznacza to, że przypadek ten ma miejsce,
gdy
a ∊ [1, 43]. Wówczas mamy W = a3mn = a3(4 − √3)(8 − 3a + √3). Szukamy
największej
możliwej wartości tego wyrażenia dla a ∊ [1, 43]. Zauważmy, że jest ona osiągana wtedy,
gdy
osiągana jest największa możliwa wartość wyrażenia a3(8 − 3a + √3) = −3a4 + (8 +
√3)a3.
Niech f(a) = −3a4 + (8 + √3)a3. Wówczas f'(a) = −12a3 + 3(8 + √3)a2. Jak łatwo
zauważyć,
pochodna f ma pierwiastek dwukrotny 0 oraz pierwiastek jednokrotny 8 + √34. Żadna z tych
liczb
nie należy do przedziału [1, 43], a zatem największa wartość f(a) w tym przedziale (a
zatem i W) jest
osiągana dla a = 1 lub a = 43. Mamy f(1) = 5 + √3 oraz f(43) = (43)3(4 +
√3) =
64(4 + √3)27 > 2(4 + √3) > 5 + √3. Zatem w tym przypadku największa możliwa wartość
wyrażenia W
wynosi 64(4 + √3)(4 − √3)27 = 83227. Pozostało rozpatrzeć przypadek, w którym po
zamianie
otrzymalibyśmy m = 4 + √3. Wówczas n = 8 − 3a − √3. Nierówność n ≥ 4 − √11 sprowadza się
do prawdziwej
nierówności a ≤ 4 + √11 − √33, a nierówność n ≤ 4 − √3 sprowadza się do nierówności
a ≥ 43.
Oznacza to, że ten przypadek ma miejsce, gdy a ∊ [43, 4 + √11 − √33] (dla a =
43 możemy
otrzymać m = 4 + √3 i n = 4 − √3). Wówczas W = a3(4 + √3)(8 − 3a − √3). Szukamy
największej
możliwej wartości tego wyrażenia dla a ∊ [43, 4 + √11 − √33]. Zauważmy, że jest
ona osiągana
wtedy, gdy osiągana jest największa możliwa wartość wyrażenia a3(8 − 3a − √3) = −3a4 +
(8 − √3)a3.
Niech g(a) = −3a4 + (8 − √3)a3. Wówczas g'(a) = −12a3 + 3(8 − √3)a2. Jak łatwo
zauważyć,
pochodna g ma pierwiastek dwukrotny a = 0 i pierwiastek jednokrotny 8 − √34. Stąd łatwo
wynika,
że funkcja f osiąga maksimum dla argumentu a = 8 − √34. Zauważmy, że argument ten należy
do przedziału [43, 4 + √11 − √33]. Oznacza to, że wyrażenie W w tym przypadku
osiągnie
maksimum dla a = 8 − √34. Wynosi ono wówczas (po przekształceniach, nie będę tego
przepisywał,
bo jest tam trochę liczenia) 14596 − 3319√3256. Nietrudno zauważyć, że liczba ta jest
większa niż
83227 (choć też trochę trzeba policzyć). Oznacza to, że szukaną największą wartością
wyrażenia W
jest 14596 − 3319√3256 i jest ona osiągana dla a = b = c = n = 8 − √34 i m = 4 +
√3.
Problem 18.
Styczne do okręgu ω w punktach A i B przecinają się w punkcie P. Punkt M jest środkiem odcinka
AP, punkt N zaś drugim punktem przecięcia prostej BM z okręgiem ω. Wykaż, że PN = 2MN.
 Oznaczmy ten punkt N' wtedy na czworokącie N"ABP można opisać okrąg?
Oznaczmy ten punkt N' wtedy na czworokącie N"ABP można opisać okrąg?

 mlutki błędzik
mlutki błędzik 


 ale takie maturalne a nie konkursowe
ale takie maturalne a nie konkursowe