.
bezendu:
Metodą operatorową rozwiązać zagadnienie początkowe y'+2y+10e
3t y(0)=7
hmm jak dalej
20 cze 20:18
52: źle przepisałeś
20 cze 20:42
bezendu:
y'+2y=10e3t y(0)=7
20 cze 21:07
52: Ogarniasz transformate Laplace'a ?
20 cze 21:21
bezendu:
Tak, a co ma do tego transformata ? Można zrobić raczej bez jej użycia chyba
20 cze 21:27
52: metoda operatorowa to laplace
20 cze 21:33
bezendu:
Nie zawsze.
20 cze 21:36
52: Z tego co kojarzę to jeśli masz metodą operatorową to Laplace z tabelki z gotowych wzorów...
Jeśli typowo Laplace to z definicji...
może ktoś się wypowie jak to jest ?
20 cze 21:39
52: mi wyszło y= 10e
3t−10e
2t
Jak zrobisz to napisz ile ci wyszło

20 cze 21:48
bezendu:
Ok.
20 cze 21:54
bezendu:
A możesz pokazać jak to liczysz ?
20 cze 22:01
20 cze 22:07
bezendu:
dzięki
20 cze 22:10
Mariusz: 5(s−3)+5(s+2)=10s−5
(s+2)−(s−3)=5
4(s−3)+6(s+2)=10s
−(s−3)+(s+2)=5
5(s−3)+2(s+2)=7s−11
| | 5(s−3)+2(s+2) | |
Y(s)= |
| |
| | (s−3)(s+2) | |
y=5e
−2t+2e
3t
20 cze 22:32
bezendu:
Dzięki Mariusz, masz jeszcze chwilkę ?
20 cze 22:36
52: | | 10 | |
Mariusz, |
| powinien być w pierwszej linijce po prawej stronie równania  |
| | s−3 | |
20 cze 22:40
bezendu:
Muszę sprawdzić poprawność
Mam całkę oznaczoną
∞
| | dx | | dx | |
∫ |
| =limε→∞∫ |
| |
| | x2+2x | | x2+2x | |
0
| | dx | | 1 | | 1 | |
∫ |
| = |
| ln|x|− |
| ln|x+2|+C |
| | x2+2x | | 2 | | 2 | |
ε
0
| | 1 | | 1 | | 1 | | 1 | |
=[ |
| ln|ε|− |
| |ε+2|]−[ |
| ln|0|− |
| |ln2|] |
| | 2 | | 2 | | 2 | | 2 | |
| | 1 | | 1 | | 1 | |
= |
| ln|ε|− |
| |ε+2|+ |
| ln|2| |
| | 2 | | 2 | | 2 | |
| | 1 | | 1 | | 1 | |
licząc limε→∞ |
| ln|ε|− |
| |ε+2|+ |
| ln|2|=∞ |
| | 2 | | 2 | | 2 | |
Zgadza się ?
20 cze 22:43
Mariusz: ups pomyliłem znak
9(s−3)−2(s+2)=7s−31
| | 9(s−3)−2(s+2) | |
Y(s)= |
| |
| | (s−3)(s+2) | |
y=9e
−2t−2e
3t
20 cze 22:43
bezendu:
sprawdzisz zadanie 22:43 ?
20 cze 22:46
52: bezendu post 22:43 nie ...
20 cze 22:47
Mariusz: Ja bym skorzystał z własności logarytmu
(różnicę logarytmów zamieniłbym na logarytm z ułamka)
20 cze 22:47
bezendu: Co jest niby nie ?
20 cze 22:47
20 cze 22:48
20 cze 22:49
52: nie
20 cze 22:50
21 cze 00:21
Mila:
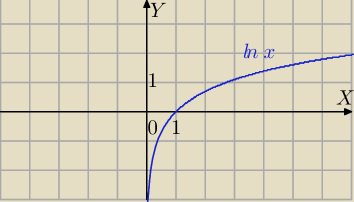
21 cze 00:23
Mila:
Nie możesz liczyć wartości ln(0), liczysz granicę dla x→0+
21 cze 00:25
Mila:
Dobranoc

Do jutra.
21 cze 00:27
52: Dobranoc

21 cze 00:27
bezendu:
Dziękuję, dobranoc
21 cze 00:32
bezendu:
Mila czli mój sposób ok ?
21 cze 17:12
Mariusz: Gdybyś zastosował to co napisałem
20 czerwca o 22:47 i policzył granice to byś dostał to co Mila
21 cze 18:27
bezendu:
Mariusz rzucisz okiem na mój inny temat. ?
21 cze 18:30
Mila:
bezendu
Chodzi o to, abyś pisał , że liczysz granice.
Nie możesz pisać, że liczysz ln0.
Poza tym to chyba lepiej mieć "zwinięte " logarytmy, czasem bardzo upraszcza się liczenie
granic.
21 cze 21:13
21 cze 21:15
bezendu:
Dobrze to mając juz
| 1 | | 1 | | 1 | |
| ln|ε|− |
| |ε+2|+ |
| ln|2| |
| 2 | | 2 | | 2 | |
przechodzę do granicy
| | 1 | | ε | | 1 | |
limε→∞ |
| ln |
| + |
| ln2 ok jak do tej pory ? |
| | 2 | | ε+2 | | 2 | |
21 cze 21:16
Mila:
Przykład:
0∫
∞e
−xdx
Obliczamy całkę nieoznaczoną:
Obliczamy całkę oznaczoną niewłaściwą:
0∫
∞e
−xdx=lim
ε→∞0∫
εe
−xdx=
=lim
ε→∞[−e
−x]
0ε=
Napisać inny przykład, gdy granica będzie równa
∞
21 cze 21:21
ZKS:
beznedu czy według Ciebie ln|0| = 0?
21 cze 21:25
bezendu:
nie istnieje
21 cze 21:25
Mila:
Za kilka minut, napiszę Twój przykład, tak, jak to widzę.
21 cze 21:26
Mila:
Witaj ZKS, onet mam już w porządku. Pozdrawiam. Z czego masz egzamin?
21 cze 21:27
ZKS:
bezendu jeżeli liczysz granice to lim
x → 0+ ln(x) = −
∞.
Mila w takim razie się cieszę mam nadzieję, że AdBlock dobrze się sprawuje.
Z Konstrukcji Betonowych tak zwany żelbet i trochę materiału mam z tego, ale mam nadzieję,
że niczego nie zapomnę.

21 cze 21:31
Mila:
Powodzenia
ZKS, AdBlock zainstalowany.
Na razie wszystko gra. Jeszcze raz dziękuje.
 bezendu
bezendu, czy wszystko jasne? Czy pisać całość jeszcze raz?
21 cze 21:43
ZKS:
Nie dziękuję, aby nie zapeszyć.

21 cze 21:44
bezendu:
Wszystko jasne, dziękuję bardzo. Też mam jutro egzamin
21 cze 22:05
bezendu:
Mila ale mi chodziło jeszczę o tą inną całkę.
∞
0
21 cze 22:07
Mila:
Właśnie o niej piszę.
Liczę całkę nieoznaczoną:
| | dx | | 1 | | ε | | 1 | | λ | |
0∫∞ |
| =lim{ε→∞} [ |
| ln( |
| )]−limλ→0[ |
| ln( |
| )=[0−(−∞)]=∞ |
| | x2+2x | | 2 | | ε+2 | | 2 | | λ+2 | |
⇔
21 cze 22:28
bezendu: Dziękuję

21 cze 22:35
Mila:
Zrozumiałeś te zapisy?
21 cze 22:43
bezendu:
Tak.
21 cze 22:51
bezendu:
Jednak nie.
Czemu jest epsilon a potem λ

21 cze 22:56
Mila:
Bo dwie różne granice, w dolnej i górnej granicy całki.
21 cze 23:15
bezendu:
Dziękuję, choć mnie uczono, że liczy się lim ∊→∞
21 cze 23:18
Mila:
Tak, ale ln z zera nie istnieje i liczysz granicę jednostronną
| | u | |
limu→0+ ln |
| =−∞ zapomniałam tam napisać 0+, |
| | u+2 | |
ale wcześniej 21 o godzinie 00:21 napisałam i wyjaśniałam z wykresem dlaczego tak jest.
21 cze 23:22
bezendu:
Dobrze, zobaczymy jak to jutro wyjdzie, mam jeszcze potem tydzień na poprawkę.
21 cze 23:23
Mila:
Będzie dobrze, najwyżej obetną jeden punkt za niezbyt precyzyjne zapisy.
Powodzenia, idź już spać. Rano wypij kawkę.
21 cze 23:26
Mila:
Dobranoc

21 cze 23:29
bezendu:
Mila nie chodzi o to, że będzie dobrze bo zdać zdam, ale mam większe ambicję w przypadku
analizy i nie mogę pozwolić sobie żeby mi gdzieś ucieli punkty.
Dziękuję jeszcze raz i dobranoc

21 cze 23:29
Mila:
Jak poszło?
23 cze 18:09
bezendu:
Wszystkie zadania zrobione, zobaczymy jak oceni pan mgr

23 cze 18:45
Hugo: u nas tylko prof 8)
23 cze 18:51



 Do jutra.
Do jutra.


 bezendu, czy wszystko jasne? Czy pisać całość jeszcze raz?
bezendu, czy wszystko jasne? Czy pisać całość jeszcze raz?





