Jak udowodnić,że czworokąt jest równoległobokiem Warettaa: Jak udowodnić, że czworokąt o wierzchołkach A(−1,2), B(3,2), C(3,4), D(−1,0) jest równoległobokiem?

J: pokazać,że odpowiednie wektory są równoległe

Warettaa: Wyznaczyć równania dwóch prostych: przechodzącej przez punkty A i B oraz przez punkty C i D?

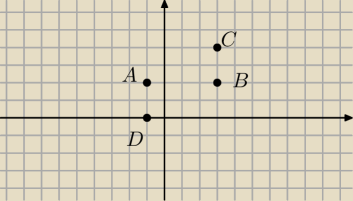
J: wektory AD i CB oraz AC i DB są parami równoległe

Warettaa: ok. Nastawiłam się na wyliczanie, więc na brudno wyliczyłam sobie prostą AB: y=−4x−6 i CD: y=x−1 i napisałam, iż proste są równoległe. Może tak zostać?

Metis: Pokaż, że wektory [AC] i [BD] są równoległe! Warunek, który muszą spełniać wektory [a₁,b₁], [a₂,b₂] a₁b₂−a₂b₁=0 Jak policzyć współrzędne wektorów: 1623

J: nie bardzo ... ja żle napisałem , odpowiednie wektory muszą być równe; AC = DB i AD = CB

Warettaa: Okej już wyliczam. Dziękuję

Metis: A sama równoległość nie wystarczy? W końcu równoległobok – czworokąt mający dwie pary równoległych boków.

J: AC i BD mogą być równoloegłe .... , ale AD i CB juz nie muszą

J: jeśli pokażemy,że są parami równoległe .... to tak ...( teraz widzę,że to już napisałem )

Metis:

Warettaa: Współrzędne wektorów: [AC]=(4,6) [DB]=(4,2) [AD]=(−2,−2) [CB]=(0,2)

Warettaa: No to się pogubiłam

J: nie ... policz jeszcze raz ( albo popatrz na rysunek, to widać) [AC] = [DB] = [4,2] [DA] = [BC] = [0,2]

Godzio: Dobrze robiłaś na początku Jak wyznaczysz wszystkie prostej i zauważysz, że odpowiednie współczynniki kierunkowe są identyczne (tzn. proste są równoległe) to znaczy, że masz równoległobok i koniec (albo wektorami tak jak piszą)

J: przecież pisanie równań prostych , to nic innego , jak liczenie współrzędnych wektorów

Godzio: A właściwie nie prostych, a wyliczenie ich współczynników kierunkowych (ale nie każdy zna wektory )

PW: Zadanie jest "nietypowe", bo autor nadał nazwy wierzchołkom "nie po kolei", wbrew zwyczajowi. Najprostszym rozwiązaniem jest pokazanie, że środki odcinków AB i DC pokrywają się:

	−1+3		2+2
MAB = (		,		) = (1, 2)
	2		2

	3+(−1)		4+0
MCD =(		,		) = (1, 2).
	2		2

Czworokąt, którego przekątne połowią się, jest równoległobokiem (znane twierdzenie, łatwe do udowodnienia za pomocą własności symetrii środkowej).