Równania wymierne jessica69: We wspólnym układzie współrzędnych narysuj wykresy funkcji: f(x) = x dla x ∊ <1;+∞) oraz 2 − x dla x ∊ (−∞;1) g(x) = ^{3x − 2}_x, gdzie x ≠ 0 Następnie rozwiąż graficznie równanie f(x) = g(x) Potrzebuję pomocy w tym równaniu f(x) = g(x). Nie wiem jak zapisać graficznie takie równanie

jessica69: J a k n a r y s o w a ć r ó w n a n i e w y m i e r n e ? Błagam o wskazówkę.

Kacper: Nie umiem rysować równań wymiernych

jessica69: Kacprze Najdroższy! Prawdopodobnie ironizujesz, w dodatku, śmiejąc się do rozpuku, ponieważ zastosowałam złą terminologię, i to diabelne równanie nie jest równaniem wymiernym, tylko jakimś cholera wie jakim. Wzywam Cię do poskromienia swojej matematycznej postawy uprzywilejowanego cynika, i proszę − zstąp na ziemię, mojej brudnej ignorancji algebraicznej i powiedz mi jak do kurwy zapisać graficznie równanie f(x) = g(x) ?

Kacper: Proszę o nie przeklinanie na forum. Rozwiązanie graficzne równania f(x)=g(x) polega na narysowaniu funkcji f(x) i g(x) w jednym układzie współrzędnych i odczytanie dla jakich x, oba wykresy funkcji osiągają tą samą wartość.

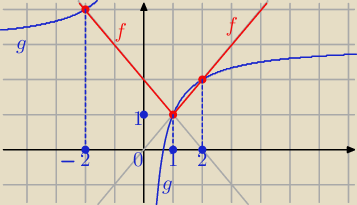
Janek191: Z wykresu odczytujemy, że f(x) = g(x) ⇔ x = − 2 lub x = 1 lub x = 2

Mila:

	3x−2
g(x)=		funkcja homograficzna, przekształcamy do postaci kanonicznej
	x

	3x		2
g(x)=		−		⇔
	x		x

	2
g(x)=3−
	x

	−2
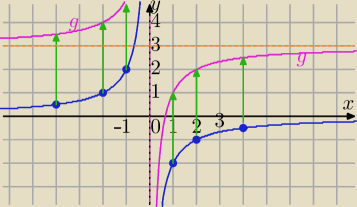
(1) rysujesz wykres y=		, x≠0
	x

( najlepiej sporządź tabelkę, jeśli nie umiesz narysowac) (2) przesuwasz cały niebieski wykres o 3 jednostki w górę. x=0 asymptota pionowa y=3 asymptota pozioma

Mila: https://matematykaszkolna.pl/strona/1485.html