Kula wpisana w stożek Kamil: Stosunek objętości stożka do objętości kuli wpisanej w ten stożek jest równy 2. Wyznacz cosinus kąta nachylenia tworzącej stożka do płażczyzny jego podstawy. Potrzebuję pomocy jak to zrobić

Kamil: Up

Eta: https://matematykaszkolna.pl/forum/132135.html

Mila:

	R		R
cosα=		=
	BC		l

	πR2*h
Vs=
	3

	4πr3
Vk=
	3

πR2*h   3
	=2⇔
4πr3   3

	R2*h
(1) R2*h=8r3⇔r3=
	8

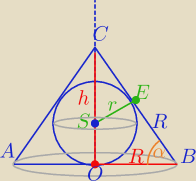
============== Z ΔBOC: h²+R²=l² h²=l²−R² h²=(l+R)*(l−R) ============ ΔCES∼ΔBOC⇔

r		R
	=		⇔r*l=R*h−r*R
h−r		l

r*l+r*R=R*h r*(l+R)=R*h

	R*h
(2) r=		/3
	l+R

	R3*h3		R2*h		R3*h3
r3=		⇔		=		⇔
	(l+R)3		8		(l+R)3

1		h2*R
	=
8		(l+R)3

1		R*(l−R)*(l+R)
	=
8		(l+R)3

1		R*(l−R)
	=
8		(l+R)2

⇔(l+R)²=8*R*(l−R) l²+2Rl+R²=8Rl−8R² l²−6Rl+9R²=0⇔ (l−3R)²=0 l=3R =====

	R
cosα=
	3R

	1
cosα=
	3

==============

Mila: II sposób, spójrz na linka Ety, będziesz miał do rozwiązania równanie trygonometryczne. Może będzie dla Ciebie łatwiejsze.