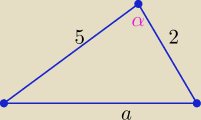
oblicz pole i obwod trojkata z tw. sinusow i cosinusow Abrakadabra: Proszę w rozwiązaniu takiego zadania: znając długości boków trójkąta : 5cm i 2 cm oraz sinus kata miedzy nimi (3/5) obliczyc pole i obwod trojkata

Qulka: jak sinα=3/5 to cosα =4/5 c² =5²+2²−2•5•2•4/5 = 25+4−16 = 13 więc trzeci bok c=√13 obwód =7+√13 Pole = 5•2•3/5 /2 = 3

Karol: Dziękuję, tylko wytłumacz dlaczego jest tak że sin=(3/5) to cos=(4/5)

J: z jedynki trygonometrycznej

Piotr: z prostego trojkata 3,4,5

Karol: aa ok, to dziękuje za rozwiązanie, już tylko jedno zadanie zostało mi na dziś i koniec dnia Jeżeli macie jeszcze siłę to prosiłbym o rozwiązanie : W trójkącie ABC dane są AC=√3 , BC=√3 , ABC=30stopni, trzeba obliczyc miary katow trojkata i dlugosc trzeciego boku trojkata

Qulka: https://matematykaszkolna.pl/strona/543.html https://matematykaszkolna.pl/strona/549.html

Karol: Dziękuje.

Piotr: przeciez to trojkat rownoramienny..

Eta:

	1
P=		*5*2*sinα=...........
	2

	3		4		4
sinα=		to cosα= ±√1−sin2α ⇒cosα=		lub cosα= −
	5		5		5

z tw. kosinusów a²= 5²+2²−2*5*2*cosα ⇒ a²= 13 ⇒ a=√13 lub

	4
a2= 52+22+2*5*2*		⇒ a2=45 ⇒ a=3√5
	5

należy jeszcze sprawdzić warunek istnienia trójkąta 5+2> √13 −−ok taki trójkąt istnieje 5+2> 3√5 −− ok taki trójkąt też istnieje i jest rozwartokątny są dwa takie trójkąty ( jeden ostrokątny a drugi rozwartokątny ) Obwody tych trójkątów: L= 7+a =.. lub L= 7+a=...

Eta: Qulka ?