Nierówność z w.bezwzględną Michcio: Podaj wartość parametru m, dla której zbiorem rozwiązań nierówności |x−3|+|x−m|≤4 jest

	1		1
przedział <1		, 5		>
	2		2

Kacper: Przenieś jedną z nierówności na drugą stronę i rób graficznie

Michcio: Mam przenieść |x−3| na prawo, narysowac 4−|x−3| Ale jak narysować |x−m| ? Nie rozumiem teraz co do mnie mówisz

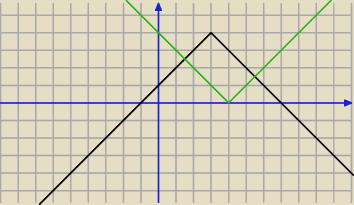Godzio: |x − m| ≤ 4 − |x − 3|

	3		11
Chcemy, żeby tylko w przedziale <		,		> wykres |x − m| był poniżej wykresu
	2		2

	3		11
4 − |x − 3|, dlatego dla argumentu x =		i x =		obie funkcje muszą przyjmować
	2		2

identyczną wartość:

	3		5		2
|		− m| =		⇒ m = −		lub m = 4
	2		2		5

	11		3
|		− m| =		⇒ m = 4 lub m = 7
	2		2

Widzimy, że oba warunki spełnione są tylko dla m = 4

Michcio: Łał dzięki Zobacz jeszcze to https://matematykaszkolna.pl/forum/294922.html czy dobrze robię Znakomicie Godzio to wytłumaczyłeś, właśnie zrobiłem podpunkt b) w tym zadaniu na bazie tego i wyszło