f.cyklometryczne tyu: mam obliczyć arcsin(x)=arccos(x) Czy tutaj mogę podzielić obustronnie przez "arc" i wtedy obliczyć dla jakiego kąta równe są funkcje sinx i cosx ?

Qulka: x=√2/2 lub −√2/2

tyu: dzięki Qulka za zainteresowanie, ale czy mogę podzielić sobie przez tego arc? Jeżeli uwzględni się zbiory wartości arccosx oraz arcsinx, to pozostaje tylko π/4

J:

	log10
Popatrz tutaj...		= 2
	log5

skróclłem przez log

5-latek: Czesc J A co wcale nie oznacza ze to jest prawda . Prawda ?

Qulka: nie możesz bo arcsin to nazwa funkcji to jakbyś chciał √2 skrócić przez pierwiastek i zostaje 2

tyu:

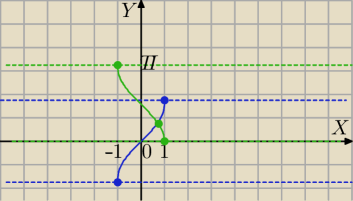
Mila: arcsinx−arccosx=0

π
	−arccosx−arccosx=0
2

π
	=2arccosx
2

	π
arccosx=
	4

	√2
x=
	2

5-latek: Dlatego pytałem czy zna teorie dotyczaca funkcji cyklometrycznych

tyu: 5−latku nie rozumiem Twojego zamiłowania do teorii Moim zdaniem to ćwiczenie czyni mistrza, a nie czytanie samej teorii, w szczególności zapisanej w sposób ścisły w podręcznikach z matematyki.

Mila: Z tym, że musisz się nauczyć rozumieć tekst matematyczny, aby zrozumieć, co do Ciebie mówią na wykładzie.

pigor: ..., widzę to ... analogicznie np. tak : arcsin(x) = arccos(x) ⇔ cos(arcsin(x)) = cos(arccos(x)) ⇔ cos(arcsin(x)) = x /² ⇔ ⇔ cos²(arcsin(x)) = x² ⇔ 1− sin²(arcsin(x)) = x ⇔ 1−x²= x² ⇔ 2x²= 1 ⇔

	1		1
⇔ √2|x|=1 ⇔ |x|=		⇔ x= ±		. ...
	√2		√2

5-latek: Czesc . To dam Ci przykład W ktoryms przykładzie zastanawiales się dlaczego rozpatrujesz przedzial <−π/2, π/2> bodajże przy funkcji y=arc sinx Gdybys jednak wiedział ze w zakresie (−∞,∞) funkcja y=sinx nie jest rozwartosciowa wiec nie możemy mowic o funkcji odwrotnej wzdledem y=sinx w tym przedziale . Ale np. w przedziale <−π/2, π/2> funkcja y=sinx jest funkcja rosnaca (wiec jest roznowartosciowa to istnieje funkcja do niej odwrotna czyli y=arc sinx

5-latek: To miedzy innymi dlatego moje zamilowanie do teorii

tyu: To w końcu dwa rozwiązania czy jedno?

tyu: 5−latku w tym przykładzie, o którym mówisz się, nad tym nie zastanawiałem dlaczego rozpatruje przedział <−π/2;π/2>, bo wiem jaki jest zbiór wartości każdej funkcji cyklometrycznej. Przeczytałem teorie i zrobiłem sobie notatki. Co do f. cyklometrycznej tak dużo teorii nie ma. Chodziło mi o cały rozumowania, w którym również napisałem o <−π/2;π/2>, bo to jest istotne. Saizou wytłumaczył mi to za pomocą definicji. Ale niech będzie, że masz rację. no a wpis "To w końcu dwa rozwiązania czy jedno?emotka z 7 cze 09:29" − ktoś się pode mnie podszywa

5-latek: Ta funkcje odwrotna możemy również oznaczyć tak x=arc siny Teraz mam jeszcze chwile czasu to napiszse CI dalej o funkcji y=arcsinx Zbiorem wartości funkcji arcsinx jest przedzial <−1,1> W przedziale tym arc sinx rosnie od −π/2 do π/2 gdyż siny rosnie od −1 do 1 gdy y zmienia się od −π/2 do π/2 Przykład arcsin √3/2=π/3 ponieważ sinπ/3=√3/2 arc sin(−0,5)=−π/6 bo sin(−π/6)=−0,5 Z definicji funkcji y=arcsinx wynika bezpośrednio ze sin(arc sinx)=x Możesz tez sobie wykazac ze arcsin(−x)= −arcsinx Rozwaz przypadki x=−1 x=1 i −1<x<1

5-latek: To nie o to chodzi ze ja mam mieć racje . To chodzi o to zebys rozumiał co liczysz . No ale skoro twierdzisz ze znasz teorie to dobrze

tyu: tu https://matematykaszkolna.pl/forum/151764.html Gustlik pisz, że zbiór wartości "ZW" (bo to chyba skrót "zbioru wartości") funkcji arcsinx to jest <−π/2;π/2> Natomiast dziedzina (skrót "D"), to tak jak piszesz <−1;1>. Ale nie będę się z Tobą spierał. post Gustlika z 25 lip 2012 10:26

5-latek: Oczywiście ze masz racje . dziedzina to <−1,1> . Pisalem to z podręcznika prof. Widolda Janowskiego Trygonometria i on w tym podręczniku piszse zamiast dziedzina pole funkcji , a zbior wartości okreslela mianem zakres funkcji . Po prostu pomylily mi się te miana. Przepraszam za pomylke

b.: pigor, 7 cze 2015 00:15: z tymi ⇔ to przesadzasz, niektóre są tylko ⇒, o czym można się łatwo przekonać podstawiając x=−1/√2.