funkcje? iii: Czy istnienieje jakiś tw. w którym występuje coś podobnego f*g=f+g ?

vaultboy: Najlepiej byłoby jakbyś wrzucił zadanie lub zagadnienie z którym masz problem.

Przemysław: Mi się skojarzyło coś takiego: (f*g)'=fg'+gf'

Bogdan: ale Przemysławie autor nie pyta o zapis z f' i g', ale z f i g

Bogdan:

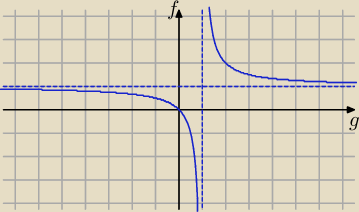
	g
fg − f = g ⇒ f(g − 1) = g ⇒ f =
	g − 1

Mamy tu do czynienia z proporcją odwrotną dla g≠1

Przemysław: Autor pytał o coś podobnego. Napisałem, że mi się skojarzyło (a czy f' czy f to już kwestia symboli). Ale oki, przepraszam za spam

Przemysław: A zresztą jak już spamuję, to co się będę hamował Bogdan gdybyś mi z tym pomógł, to byłym wdzięczny https://matematykaszkolna.pl/forum/294188.html

pigor: ..., a dla mnie to istnieje taka funkcja f(x)=log_px, że log_p(ab)= log_pa+log_pb oczywiście przy odpowiednich założeniach (jakich ?). ...

ICSP: Równania funkcyjne Cauchego ?

Ada: hmm... ale tu chodzi ci o to, czy jest takie działanie zdefiniowane, czy pytanie o istnienie (ewentualne szukanie takich funkcji?) PS Mi się to strasznie ze splotem przez znaczek kojarzy

Bogdan: To pigorze jest inny przypadek, u Ciebie f = log_pa, g = log_pb, ale wtedy chodziłoby o zapis log_ba * log_pb = og_ba + log_pb

Bogdan: Tu http://www-users.mat.umk.pl/~anow/ps-dvi/si-krl-p.pdf jest ciekawy materiał o liczbach naturalnych, których suma równa się iloczynowi.